Diskrečioji ribinė teorema Epšteino dzeta funkcijai

Įvadas

Dirichlė (Dirichlet) eilutės yra vienas iš svarbiausių ir plačiai naudojamų įrankių šiuolaikinėje skaičių teorijoje. Jos yra pagrindinis įrankis, nagrinėjant pirminių skaičių pasiskirstymą, modulinių formų problemas bei daugelyje kitų sričių. Kompleksinio kintamojo funkcijos, tam tikroje pusplokštumėje apibrėžiamos Dirichlė eilutėmis

vadinamos dzeta, arba 𝐿, funkcijomis. Čia – kompleksinių skaičių seka, – nemažėjanti realiųjų skaičių seka, tokia, kad . Tokio tipo eilutės vadinamos bendrosiomis Dirichlė eilutėmis. Jeigu , turime paprastąją Dirichlė eilutę

Vokiečių matematikas Epšteinas (P. Epstein) siekė rasti kuo bendresnę dzeta funkciją, turinčią Rymano tipo funkcinę lygtį. 1903 m. jis apibrėžė tam tikro tipo Dirichlė eilutę, vėliau pavadintą jo vardu [6]. Šios funkcijos savybes bei elgesį studijavo ir daug kitų matematikų: Hekė (E. Hecke) [9], Čovla (S. Chowla) ir Selbergas (A. Selberg) [4], Fomenko (O. M. Fomenko) [7], Nakamura (T. Nakamura) ir Pankovskis (Ł. Pańkowski) [12] ir kiti. Epšteino dzeta funkcija naudojama ir taikomuosiuose moksluose, pavyzdžiui, kvantinėje fizikoje [5].

Tegul yra teigiamai apibrėžta kvadratinė matrica. Sveikųjų skaičių rinkiniui pažymėkime . Epšteino dzeta funkcija , susieta su kvadratine matrica , apibrėžiama eilute

ir yra analiziškai pratęsiama į visą kompleksinę plokštumą.

Dzeta funkcijų reikšmių pasiskirstymo klausimai yra labai sudėtingi, todėl šioms problemoms spręsti įprastai naudojami tikimybiniai metodai. Tikimybinių metodų taikymo idėja Dirichlė eilučių reikšmių pasiskirstymui priklauso Borui (H. Bohr) ir Jesenui (B. Jessen) (žr. [2] ir [3]). Jie nagrinėjo Rymano dzeta funkcijos reikšmių pasiskirstymą. Boro ir Jeseno tyrimai yra tęsiami naudojant kitus metodus. Pavyzdžiui, tam tikrų analogiškų rezultatų pateikė Borhsenius (V. Borchsenius) ir Jesenas (B. Jessen), Jesenas ir Vinteris (A. Winter). Tačiau išvysčius tikimybinių matų silpnojo konvergavimo teoriją, pastebėta, kad dzeta funkcijų asimptotinės savybės geriausiai nusakomos tikimybinėmis ribinėmis teoremomis silpnojo tikimybinių matų konvergavimo prasme.

Tolydaus tipo ribinę teoremą Epšteino dzeta funkcijai kompleksinėje plokštumoje įrodė Laurinčikas ir Macaitienė [11]. Tačiau diskretaus tipo rezultatai turi kur kas platesnį pritaikymą, pavyzdžiui, fizikoje, kristalografijoje ar pan. Tolydaus tipo teoremose postūmiai įgyja realias reikšmes, diskretaus tipo atveju – imami iš tam tikrų diskrečiųjų aibių (pavyzdžiui, aritmetinės progresijos).

Tyrimo tikslas – įrodyti diskretaus tipo ribinę teoremą silpnojo tikimybinių matų konvergavimo prasme Epšteino dzeta funkcijai kompleksinėje plokštumoje.

Straipsnyje įrodyta, kad fiksuotam ir , tikimybinis matas

kai , silpnai konverguoja į tam tikrą ribinį matą. Pateikiamas išreikštinis ribinio mato pavidalas.

Tyrimo metodai. Diskrečiųjų ribinių teoremų įrodymai remiasi Epšteino dzeta funkcijos bei silpnojo tikimybinių matų konvergavimo savybėmis. Naudojami kontūrinio integravimo, aproksimavimo bei ergodinės teorijos metodai, Galagherio (Gallagher) lema. Priklausomai nuo aritmetinės h prigimties, nagrinėjami du skirtingi atvejai.

Epšteino dzeta funkcija

Kaip jau minėjome įvade, Epšteino dzeta funkcija apibrėžiama eilute

ir gali būti analiziškai pratęsiama į visą kompleksinę plokštumą, išskyrus paprastąjį polių taške su reziduumu . Funkcija tenkina funkcinę Rymano tipo lygtį:

,

čia yra Oilerio gama funkcija. Iš čia nesunku pastebėti, kad Epšteino dzeta funkcija lygi nuliui taškuose ; šie nuliai vadinami trivialiaisiais. Kiti nuliai yra netrivialūs. Apie jų išsidėstymą žinome kur kas mažiau, nei apie Rymano dzeta funkcijos, tačiau pastebima, kad priklauso nuo matricos . Pavyzdžiui, imkime n-matę vienetinę matricą . Tuomet Epšteino dzeta funkcija išreiškiama Rymano dzeta ir Dirichlė 𝐿-funkcijos , tiesine kombinacija. Tuomet turime, jog:

,

,

čia yra Dirichlė 𝐿-funkcija su pagrindiniu Dirichlė charakteriu moduliu 4. Pastebime, kad jei teisinga Rymano hipotezė, tai visi netrivialūs nuliai yra kritinėje tiesėje . Jei Rymano hipotezės analogas galioja Dirichlė 𝐿-funkcijai , tuomet visi netrivialūs nuliai yra ant tiesių ir . Analogiškai, jei teisinga Rymano hipotezė ir jos analogas Dirichlė 𝐿-funkcijai, tuomet netrivialūs nuliai yra ant tiesių , bei be galo daug nulių taške . Tiesės ir vadinamos kritinėmis tiesėmis. Tačiau sudėtingesnių matricų atveju, nulių išsidėstymas yra kur kas sudėtingesnis.

Svarbu akcentuoti, jog gali būti užrašoma paprastąja Dirichlė eilute. Pažymėkime viršutinę pusplokštumę , – pilną modulinę grupę

,

o sveikiesiems teigiamiems , jos pogrupį

,

kuris vadinamas Hekės pogrupiu arba kongruenčiuoju pogrupiu . Be to, tegul yra analizinė viršutinėje pusplokštumėje funkcija. Jeigu visiems elementams funkcija tenkina funkcinę lygtį

ir yra analizinė paraboliniuose taškuose, tuomet vadinama svorio ir lygio moduline forma. Jei virsta 0 visuose paraboliniuose taškuose, tuomet ji vadinama paraboline forma. Pažymėkime Eisenšteino eilutę

Tarkime, kad yra sveikasis skaičius su kiekvienu sveikųjų skaičių rinkiniu .

Pažymėkime , elementų , tenkinančių žemiau pateiktą reikalavimą, skaičių, t. y.

.

Tuomet pusplokštumėje Epšteino dzeta funkcija gali būti užrašoma paprastąja Dirichlė eilute

Fomenko įrodė [7], jog eilutės

yra svorio modulinės formos ir jos gali būti išreiškiamos atitinkamos Eisenšteino eilutės ir tam tikros parabolinės formos suma:

,

kur yra Eisenšteino eilutė, o – parabolinė forma. Iš čia seka, kad Epšteino dzeta funkcija gali būti išreikšta atitinkamų dzeta funkcijų suma:

kur

Įrodant ribinę teoremą, šis išskaidymas vaidina ypatingai svarbų vaidmenį. Ivaniec įrodė [10], jog lyginiams Eisenšteino eilutė yra svorio ir lygio modulinė forma. Be to, Hekė įrodė [9], jog dzeta funkcija gali būti išreiškiama elementų tiesine kombinacija, kur k ir l yra q dalikliai, ir – Dirichlė charakteriai moduliu ir . Iš čia ir lygybės seka, jog pusplokštumėje , Epšteino dzeta funkcija išreiškiama Dirichlė L-funkcijų tiesine kombinacija:

čia yra kompleksiniai skaičiai, o ir yra neekvivalentūs charakteriai. Be to, jei galioja įvertis

tai eilutė konverguoja absoliučiai pusplokštumėje

Diskrečioji ribinė teoremaEpšteinodzeta funkcijai

Kaip jau minėta, Laurinčikas ir Macaitienė [11] įrodė, kad

kai , silpnai konverguoja į tam tikrą tikimybinį matą P. Čia yra mačios aibės A Lebego matas, o žymi erdvės Borelio aibių klasę.

Mūsų tikslas yra pateikti diskretaus tipo rezultatą, kai t reikšmės yra imamos iš aritmetinės progresijos. Pateiksime ir išreikštinį ribinio mato pavidalą. Ribinio mato apibrėžimui taikoma speciali topologinė struktūra. Apibrėžkime aibę

kur visiems pirminiams skaičiams p. Su sandaugos topologija ir pataškine daugyba toras yra kompaktiška topologinė Abelio grupė. Todėl erdvėje egzistuoja tikimybinis Haro matas , taigi, turime tikimybinę erdvę . Tegul žymi p-ąjį elemento komponentą, t. y. yra elemento projekcija į Funkcijos apibrėžimo sritį iš išplečiame į natūraliųjų skaičių aibę :

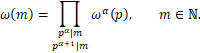
Tuomet tikimybinėje erdvėje apibrėžiame kompleksines reikšmes įgyjantį atsitiktinį elementą

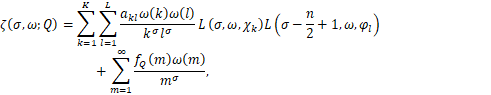
kur atitinkamos Dirichlė L funkcijos yra išreiškiamos tolygiai konverguojančiomis Oilerio sandaugomis (beveik visiems ):

ir

Laurinčikas ir Macaitienė įrodė [11], jog minėtas ribinis matas yra šio atsitiktinio elemento skirstinys.

Diskretusis atvejis yra sudėtingesnis nei tolydusis, nes priklauso nuo skaičiaus aritmetinės prigimties. Nagrinėjami du atvejai: kai yra toks, kad yra iracionalusis skaičius (1-asis h tipas) ir kai yra toks, kad nėra iracionalusis skaičius (2-asis h tipas), visiems . Sakykime, kad yra 2-ojo tipo. Tuomet nesunku pastebėti, kad egzistuoja toks mažiausias , kad skaičius yra racionalusis skaičius. Pavyzdžiui, jei , pagal Hermitės-Lindemano teoremą, yra transcendentinis skaičius visiems . Kai , tuomet yra racionalusis skaičius. Tarkime, kad Pažymėkime pirminių skaičių aibės poaibį:

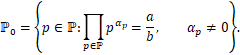
Be to, tegul žymi uždarą grupės pogrupį, generuotą . Akivaizdu, jog yra kompaktiška grupė, tuomet erdvėje egzistuoja tikimybinis Haro matas . Turime tikimybinę erdvę . Remiantis Bagchi lema [1, 4.2.2 lema],

Dabar tikimybinėjė erdvėje apibrėžkime kompleksines reikšmes įgyjantį atsitiktinį elementą

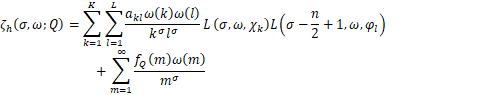
ir pažymėkime šio atsitiktinio elemento pasiskirstymą:

Be to, tegul A žymi aibės A elementų skaičių. Pagrindinis rezultatas yra žemiau pateikta diskrečioji Boro-Jeseno tipo ribinė teorema funkcijai kompleksinėje plokštumoje.

Teorema. Tarkime, kad ir visiems yra lyginis skaičius. Tuomet, su fiksuota reikšme, tikimybinis matas

kai , silpnai konverguoja į .

Teorema įrodyta B. Gutauskienės magistro darbe [8].

Išvados

Straipsnyje pateikiamas diskretaus tipo tikimybinis rezultatas, kad fiksuotam matas

kai , silpnai konverguoja į atsitiktinio elemento skirstinį. Diskretusis atvejis yra kur kas sudėtingesnis, nei tolydusis (įrodytas [11]), kadangi priklauso nuo aritmetinės prigimties. Nagrinėti du atvejai [8]: kai yra racionalusis ir iracionalusis skaičiai, visiems .

Planuojama įrodyti apibendrintą diskretųjį atvejį, kai postūmiai iš aritmetinės progresijos keičiami tam tikra bendresne funkcija.