Problemos ISSN 1392-1126 eISSN 2424-6158

2023, vol. 103, pp. 145–154 DOI: https://doi.org/10.15388/Problemos.2023.103.11

Vertimai / Translations

Semantiniai svarstymai apie modalinę logiką

Saul A. Kripke
Harvardo universitetas

Iš anglų kalbos vertė ir pratarmę parašė Pranciškus Gricius, Vilniaus universitetas

Saulo Kripkės (1940–2022) straipsnis, kurio lietuviškas vertimas pristatomas skaitytojams, – tai vienas iš pamatinių modalinės logikos tyrimų. Jame pirmąsyk detaliai išplėtota šiuolaikinė kvantorinės modalinės logikos semantika, formaliai identifikuoti skirtingų šios logikos sistemų semantiniai loginio sekmens sąryšiai, pateiktos šiems sąryšiams adekvačios, t. y. išsamios ir neprieštaringos, aksiomatinės sistemos. Ko gero, kertinė Kripkės idėja yra ta, kad modalumus būtina ir galima derėtų interpretuoti ne kaip kvantorius, kurių sritis yra nemodaliniai modeliai, o kaip kvantorius, kurių sritis priklauso nuo pačiuose modeliuose esančių modalinių dėmenų – galimų pasaulių ir prieinamumo sąryšio tarp jų. Ši idėja jam leido parodyti keletą svarbių dalykų. Pirma, kiekvienam galimam pasauliui priskyrus (galimai vis kitą) individų aibę ir įvedus šioms aibėms jautrius aktualistinius kvantorius, Kripkės išplėtota semantika leido jam formaliai nustatyti sąlygas, kurioms galiojant Barcan formulė ir (ar) jos konversija yra (nėra) tapačiai teisinga. Antra, ši idėja leido parodyti, kad modalumai yra ne metalingvistinės, o metafizinės prigimties, tai savo ruožtu sudarė sąlygas suformuluoti ir pagrįsti pamatinius argumentus už visą pluoštą tezių kalbos filosofijoje ir metafizikoje, pavyzdžiui, argumentus, išsakytus Kripkės paskaitose Vardai ir būtinumas, už tai, kad vardai yra rigidiniai designatoriai, už semantinį eksternalizmą, esencializmą ir pan.

Pristatomas tekstas pirmą kartą buvo publikuotas Suomijos filosofų draugijos leidinyje Acta Philosophica Fennica 1963 metais, o 1971-aisiais perspausdintas Leonardo Linsky sudarytoje rinktinėje Referencija ir modalumai. Esama nedidelių skirtumų tarp dviejų teksto leidimų. Keli iš jų verti paminėti: pateikdamas modalinės teiginių logikos aksiomatinę sistemą (žr. p. 146 toliau), Kripkė įtraukia aksiomą A0 tik 1971-ųjų leidime; antra išnaša (žr. p. 148 toliau) pasirodo 1963 m., o 1971-ųjų leidime jos nėra.

Versta iš:
Saul A. Kripke. 1963. Semantical Considerations on Modal Logic.
Acta Philosophica Fennica 16: 83–94.

_________

Padėka. Finansavimą skyrė Vilniaus universiteto Mokslo skatinimo fondas, sutarties Nr. MSF-JM-24/2022. Taip pat dėkoju profesoriui Jonui Dagiui ir daktarei Živilei Pabijutaitei už išsamius ir vertingus pastebėjimus, kolegišką paramą kuriant ir gludinant lietuvišką modalinės logikos terminiją.

Copyright © Saul A. Kripke. Translation from English to Lithuanian, preface Copyright © Pranciškus Gricius, 2023.
Published by Vilnius University Press. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

_________

Straipsnyje aprašomos kelios modalinių logikų semantinės teorijos ypatybės¹. Tokia teo­rija, skirta tam tikram kvantoriniam S5 plėtiniui, jau buvo pristatyta (Kripke 1959a) ir apibendrinta (Kripke 1959b). Šiame straipsnyje susitelkiama į vieną šios teorijos aspektą – kvantorių įvedimą – ir didžia dalimi apsiribojama vienu metodu šiam tikslui pasiekti. Straipsnyje daugiausia dėmesio skiriama grynai semantiniams klausimams, tad čia nebus naudojamos semantinės lentelės (semantic tableaux), kurios yra būtinos išsamiam teorijos išdėstymui (apie lenteles žr. Kripke 1959a ir 1963). Įrodymai taip pat dažniausiai bus praleidžiami.

Nagrinėsime keturias modalines sistemas. Formulės A, B, C, ... sudaromos iš atominių formulių P, Q, R, ... naudojant jungtis ∧, ~ ir ◻. Sistemoje M yra šios aksiomų schemos ir taisyklės:

A0. funkcinės teisingumo atžvilgiu tautologijos

A1. ◻ A ⊃ A

A2. ◻ (A ⊃ B) . ⊃ . ◻A ⊃ ◻B

R1. A, A ⊃ B / B

R2. A / ◻A

Jei pridedame aksiomų schemą

◻A →◻◻A,

tai gauname S4. Brauerišką sistemą gauname prie M pridėję:

A →◻◊A.

S5, jei pridedame:

◊A→◻◊A.

Modalinės sistemos, kurių teoremos yra uždaros pagal taisykles R1 ir R2 (closed under the rules R1 and R2) ir kurios įtraukia visas M teoremas, yra vadinamos „normaliomis“. Nors anksčiau išplėtojome teoriją, kurioje galima analizuoti tokias nenormalias sistemas kaip Lewiso S2 ir S3, šiame straipsnyje apsiribosime vien normaliomis sistemomis.

Norėdami pateikti semantiką modalinei logikai, įvedame (normalios) modelių struktūros sąvoką. Modelių struktūra (m. s.) yra sutvarkytas trejetas (G, K, R), kuriame K yra aibė, R – tai aibės K refleksyvus sąryšis ir G ∊ K. Intuityviai į reikalą žvelgiame taip: K yra visų „galimų pasaulių“ aibė, G yra „tikrasis pasaulis“. Jei H₁ ir H₂ yra du pasauliai, tai H₁ R H₂ intuityviai reiškia, kad H₂ yra „galimas atžvilgiu“ (possible relative to) H₁, t. y. kad kiekvienas teiginys, kuris yra teisingas pasaulyje H₂, yra galimas pasaulyje H₁. Tokiu būdu aišku, kad sąryšis R išties turėtų būti refleksyvus: kiekvienas pasaulis H yra galimas savo paties atžvilgiu, kadangi kiekvienas teiginys, kuris yra teisingas pasaulyje H, a fortiori, yra galimas pasaulyje H. Tad refleksyvumo reikalavimas yra intuityviai natūralus. Galime kelti ir papildomų reikalavimų, kurie atitinka įvairias modalinės logikos „redukcijos aksiomas“: jei R tranzityvus, tai (G, K, R) vadinsime S4-m. s.; jei R simet­riškas, tai (G, K, R) yra braueriška m. s.; o jei R yra ekvivalentumo sąryšis, tai (G, K, R) vadinsime S5-m. s. Modelio struktūra, kuriai nekeliame jokių reikalavimų, taip pat vadinama M-modelio struktūra.

Išsamiam vaizdui reikalingas modelio apibrėžimas. Kai duota modelių struktūra (G, K, R), tai modelis kiekvienai atominei formulei (propoziciniam kintamajam) P priskiria teisingumo reikšmę T arba F kiekviename pasaulyje H ∊ K. Formaliai modelių struktūros (G, K, R) modelis φ – tai dvivietė funkcija φ(P, H), kurios reikšmių sritis yra aibė {T, F}, kur P reikšmių sritis yra atominės formulės, o H reikšmių sritis – aibės K elementai. Kai duotas modelis, galime induktyviai apibrėžti, kaip teisingumo reikšmės priskiriamos neatominėms formulėms. Tarkime, kad φ(A, H) ir φ(B, H) jau yra apibrėžtos visiems H ∊ K. Tada, jei φ(A, H) = φ(B, H) = T, apibrėžiame φ(A ∧ B, H) = T; priešingu atveju φ(A ∧ B, H) = F. Apibrėžiame, kad φ(~A, H) yra F, jei ir tik jei φ(A, H) = T; priešingu atveju φ(~A, H) = T. Galiausiai, apibrėžiame, jog φ(◻A, H) = T, jei ir tik jei φ(A, H′) = T kiekviename H′ ∊ K, kuris H R H′; priešingu atveju φ(◻A, H) = F. Intuityviai tai reiškia, kad A yra būtina pasaulyje H, jei ir tik jei A yra teisinga visuose pasauliuose H′, kurie yra galimi H atžvilgiu.

Pilnumo teorema. ⊢ A [sistemoje] M (S4, S5, braueriškoje sistemoje), jei ir tik jei φ(A, G) = T kiekviename M-(S4-, S5-, braueriškos) modelio struktūros (G, K, R) modelyje φ.

(Įrodymą žr. Kripke 1963).

Ši pilnumo teorema sintaksinę įrodomumo (provability) modalinėje sistemoje sąvoką sulygina (equates) su semantine tapataus teisingumo (validity) sąvoka.

Likusi straipsnio dalis, išskyrus keletą baigiamųjų pastabų, skirta kvantorių įvedimui. Šiam tikslui turime su kiekvienu pasauliu susieti tam tikrą individų sritį – tokių individų, kurie tame pasaulyje egzistuoja. Formaliai kvantorinę modelio struktūrą (k. m. s.) apibrėžiame kaip modelio struktūrą (G, K, R) kartu su funkcija ψ, kuri kiekvienam H ∊ K priskiria aibę ψ(H), vadinamą H sritimi. Intuityviai ψ(H) yra visų pasaulyje H egzistuojančių individų aibė. Tarp kitko, verta pastebėti, jog skirtingiems argumentams H aibė ψ(H) neturi būti ta pati, lygiai taip, kaip intuityviai kituose nei tikrasis pasauliuose gali nebūti kai kurių faktiškai egzistuojančių individų ir gali atsirasti naujų individų, tokių kaip Pegasas.

Tada prie modalinės logikos simbolių galime pridėti begalinį sąrašą individinių kintamųjų x, y, z, ... bei kiekvienam teigiamam sveikajam skaičiui n sąrašą n-viečių predikatinių raidžių Pⁿ, Qⁿ, ..., kurių indeksas (superscript) kartais suprantamas iš konteksto. Propozicinius kintamuosius (atomines formules) laikysime „0-vietėmis“ predikatinėmis raidėmis. Tada taisyklingai sudarytas formules konstruojame įprastu būdu ir galime ruoštis apibrėžti kvantorinį modelį.

Tam, kad apibrėžtume kvantorinį modelį, turime praplėsti ankstesnę sąvoką, pagal kurią teisingumo reikšmė priskiriama kiekvienai atominei formulei kiekviename pasaulyje. Analogiškai tam, turime tarti, kad kiekviename pasaulyje duotoji n-vietė predikatinė raidė apibrėžia tam tikrą aibę sutvarkytų n-viečių aibių, t. y. jos ekstensiją tame pasaulyje. Aptarkime, pavyzdžiui, vienvietės predikatinės raidės P(x) atvejį. Norėtume sakyti, kad pasaulyje H predikatas P(x) yra teisingas kai kuriems individams iš ψ(H) ir klaidingas kitiems. Formaliai sakytume, kad tam tikrų ψ(H) elementų priskyrimo (assignments) kintamajam x atžvilgiu φ(P(x), H) = T, o kitų priskyrimų atžvilgiu φ(P(x), H) = F. Aibė visų individų, kuriems P yra teisinga, vadinama P ekstensija pasaulyje H. Bet čia kyla problema: ar derėtų priskirti teisingumo reikšmę φ(P(x), H), kai kintamajam x priskiriama reikšmė iš kokio nors kito pasaulio H′ srities, bet ne iš H srities? Intuityviai tarkime, kad P(x) reiškia „x yra nuplikęs“ – ar priskirtume teisingumo reikšmę P(x) substituciniam atvejui „Šerlokas Holmsas yra nuplikęs“? Holmsas neegzistuoja, bet susiklosčius kitoms dalykų padėtims jis būtų egzistavęs. Ar turime priskirti apibrėžtą teisingumo reikšmę teiginiui, kad jis yra nuplikęs, ar ne? Frege (1892) ir Strawsonas (1950) šiam sakiniui (statement) nepriskirtų jokios teisingumo reikšmės, o Russellas (1905) priskirtų². Atsižvelgdami į modalinės logikos tikslus, laikome, kad skirtingi atsakymai į šį klausimą reprezentuoja alternatyvias konvencijas. Visos jos yra įmanomos. Vieninteliuose darbuose, kiek teko matyti, kuriuose svarstoma ši problema – Hintikkos (1961) ir Prioro (1957) – priimama Fregės–Strawsono pozicija. Ši pozicija verčia keisti įprastą modalinę logiką. Taip yra dėl to, kad modalinės teiginių logikos semantika, kurią pateikėme anksčiau, numato, kad kiekviena formulė kiekviename pasaulyje įgyja teisingumo reikšmę. O štai Fregės–Strawsono pozicija reikalauja nepriskirti jokios teisingumo reikšmės formulei A(x) su laisvu kintamuoju x pasaulyje H, jei kintamajam x priskirtas individas, kurio nėra to pasaulio srityje. Tad nebegalime tikėtis, kad pradiniai (original) modalinės teiginių logikos dėsniai galios teiginiams su laisvais kintamaisiais, ir privalome rinktis: arba keisti modalinę teiginių logiką, arba apriboti substitucijos taisyklę. Prioras renkasi pirmąjį kelią, o Hintikka – antrąjį. Fregės–Strawsono pasirinkimas reikalauja ir kitų sprendimų: ar derėtų teigti, kad ◻A (pasaulyje H) reiškia tai, jog A yra teisinga visuose galimuose (H atžvilgiu) pasauliuose, ar tik tai, kad A nėra klaidinga nė viename iš šių pasaulių? Pastaroji alternatyva reikalauja tik tiek, kad kiekviename pasaulyje A būtų arba teisinga, arba neturėtų teisingumo reikšmės. Prioras savo sistemoje Q pripažįsta abu būtinumo tipus: vieną kaip „L“, o kitą kaip „NMN“. Panašus klausimas kyla dėl konjunkcijos: jei A yra klaidinga, o B neturi teisingumo reikšmės, tai ar turėtume manyti, kad A ∧ B yra klaidinga, ar kad ji teisingumo reikšmės neturi?

Išsamiame semantinės teorijos išdėstyme aptartume visus šiuos galimus Fregės–Strawsono pozicijos variantus. Čia renkamės kitą kelią ir darome prielaidą, kad sakinys su laisvais kintamaisiais turi teisingumo reikšmę kiekviename pasaulyje kiekvieno [reikšmių] priskyrimo jo laisviems kintamiesiems atžvilgiu³. Formaliai tai apibrėžiame taip: tegu 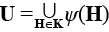. Uⁿ – tai n-toji dekartiška aibės U sandauga su ja pačia. Kvantorinį modelį kvantorinėje modelių struktūroje (G, K, R) apibrėžiame kaip dvivietę funkciją φ(Pⁿ, H), kur kintamojo Pⁿ reikšmių sritis yra n-vietės predikatinės raidės laisvai parinktam n, o kintamojo H reikšmių sritis yra aibės K elementai. Jei n = 0, tai φ(Pⁿ, H) = T arba F, o jei n ≥ 1, tai φ(Pⁿ, H) yra aibės Uⁿ poaibis. Dabar induktyviai apibrėžiame teisingumo reikšmę φ(A, H) kiekvienai formulei A ir H ∊ K duotojo U elementų priskyrimo laisviems kintamiesiems formulėje A atžvilgiu. Propozicinių kintamųjų atvejis yra akivaizdus. Atominei formulei Pⁿ(x₁, ..., x_n), kur Pⁿ yra n-vietė predikatinė raidė ir n ≥ 1, jei duotas a₁, ..., a_n elementų iš U priskyrimas kintamiesiems x₁, ..., x_n, apibrėžiame φ(Pⁿ(x₁, ..., x_n), H) = T, jei sutvarkytoji aibė (a₁, ..., a_n) yra aibės φ(Pⁿ, H) narys; priešingu atveju, duotojo priskyrimo atžvilgiu, φ(Pⁿ(x₁, ..., x_n), H) = F. Jei šios reikšmės yra priskirtos atominėms formulėms, sudėtinėms formulėms priskirtinas reikšmes galima nustatyti pagal indukciją. Jau buvo pateikti indukcijos žingsniai propozicinėms jungtims ∧, ~, ◻. Tarkime, kad turime formulę A(x, y₁, ..., y_n), kur x ir y_i yra vieninteliai laisvi kintamieji, ir kad teisingumo reikšmė φ(A(x, y₁, ..., y_n), H) jau yra apibrėžta kiekvienam [reikšmių] priskyrimui laisviems kintamiesiems formulėje A(x, y₁, ..., y_n). Tada apibrėžiame φ((x)A(x, y₁, ..., y_n), H) = T, atžvilgiu [reikšmių] b₁, ..., b_n priskyrimo kintamiesiems y₁, ..., y_n (kai b_i yra U nariai), jei φ(A(x, y₁, ..., y_n), H) = T kiekvieno [reikšmių] a, b₁, ..., b_n priskyrimo, atitinkamai, kintamiesiems x, y₁, ..., y_n atžvilgiu, kur a ∊ ψ(H); priešingu atveju, duotojo priskyrimo atžvilgiu, φ((x)A(x, y₁, ..., y_n), H) = F. Atkreipkime dėmesį: reikalavimas, kad a ∊ ψ(H), reiškia, jog pasaulyje H į kvantorių veikimo sritį patenka tik tie objektai, kurie faktiškai egzistuoja H.

Šią semantiką iliustruosime pateikdami kontrapavyzdžius dviem gerai pažįstamiems pretendentams į modalinės kvantifikavimo teorijos dėsnius – „Barcan formulei“ (x)◻A(x) ⊃ ◻(x)A(x) ir jos konversijai ◻(x)A(x) ⊃ (x)◻A(x). Kiekvienai jų aptarsime modelio struktūrą (G, K, R), kur K = {G, H}, G ≠ H, o R – tiesiog dekartiška sandauga K². Akivaizdu, kad sąryšis R yra refleksyvus, tranzityvus ir simetriškas, tad mūsų aptarimas galioja net ir S5.

Barcan formulei praplečiame (G, K, R) iki kvantorinės modelių struktūros, apibrėždami ψ(G) = {a}, ψ(H) = {a, b}, kur a ir b nėra tapatūs. Paskui vienvietei predikatinei raidei P apibrėžiame modelį φ, kuriame φ(P, G) = {a}, φ(P, H) = {a}. Tada akivaizdu, kad ◻P(x) yra teisinga pasaulyje G, jei kintamajam x priskirta [reikšmė] a, o kadangi a yra vienintelis objektas pasaulio G srityje, tai teisinga ir (x)◻P(x). Tačiau pasaulyje H formulė (x)P(x) yra aiškiai klaidinga (nes φ(P(x), H) = F, jei kintamajam x priskirta [reikšmė] b), ir dėl to formulė ◻(x)P(x) yra klaidinga pasaulyje G. Taigi, turime kontrapavyzdį Barcan formulei. Atkreipkite dėmesį į tai, kad šis kontrapavyzdys visiškai nepriklauso nuo to, ar pasaulyje G formulei P(x) yra priskiriama kokia nors teisingumo reikšmė ar ne, jei kintamajam x priskirta [reikšmė] b, tad šis kontrapavyzdys taip pat veikia Hintikkos ir Prioro sistemose. Tokie kontrapavyzdžiai pasidarytų nepriimtini ir Barcan formulės statusas būtų atkurtas, tik jei reikalautume, kad modelių struktūra atitiktų sąlygą, kad ψ(H′) ⊆ ψ(H), visada, kai H R H′ (H, H′ ∊ K).

Barcan formulės konversijai nustatykime ψ(G) = {a, b}, ψ(H) = {a}, kur vėlgi a ≠ b. Apibrėžkime φ(P, G) = {a, b}, φ(P, H) = {a}, kur P yra duotoji vienvietė predikatinė raidė. Tada aišku, kad formulė (x)P(x) yra teisinga ir pasaulyje G, ir pasaulyje H, todėl φ(◻(x)P(x), G) = T. Bet kai kintamajam x priskiriama [reikšmė] b, tai φ(P(x), H) = F, ir todėl, kai kintamajam x priskiriama reikšmė b, φ(◻P(x), G) = F. Taigi, φ((x)◻P(x), G) = F, ir mes gavome pageidaujamą kontrapavyzdį Barcan schemos konversijai. Tačiau šis kontrapavyzdys remiasi prielaida, kad, kai kintamajam x priskirta [reikšmė] b, formulė P(x) pasaulyje H iš tikrųjų yra klaidinga. Jei būtų nuspręsta, kad to paties priskyrimo atžvilgiu formulė P(x) pasaulyje H teisingumo reikšmės neturi, šio kontrapavyzdžio nebeliktų. Šiuo atveju kontrapavyzdys galios, jei reikalausime, kad būtinas teiginys visuose galimuose pasauliuose būtų teisingas (Prioro „L“), bet negalios, jei reikalausime tik to, kad jis niekuomet nebūtų klaidingas (Prioro „NMN“). Pagal dabartinę mūsų konvenciją, tokius kontrapavyzdžius pašalinti galime tik reikalaudami kiekvienai k. m. s., kad ψ(H) ⊆ ψ(H′), visada, kai H R H′.

Šie kontrapavyzdžiai sukelia savitą keblumą: pateikėme kontramodelius Barcan schemai ir jos konversijai kvantorinėje S5 sistemoje. Tačiau panašu, kad dar Prioras (1956) parodė, kad Barcan formulė yra išvedama kvantorinėje S5, o jos konversija atrodo išvedama net kvantorinėje M pagal tokį samprotavimą:

(A) (x)A(x) ⊃ A(y) (pagal kvantifikavimo teoriją);

(B) ◻((x)A(x) ⊃ A(y)) (pagal būtinumo įvedimą (necessitation));

(C) ◻((x)A(x) ⊃ A(y)) ⊃ ◻(x)A(x) ⊃ ◻A(y) (aksioma A2);

(D) ◻(x)A(x) ⊃ ◻A(y) (iš (B) ir (C));

(E) (y)(◻(x)A(x) ⊃ ◻A(y)) (apibendrinant (D));

(F) ◻(x)A(x) ⊃ (y)◻A(y) (pagal kvantifikavimo teoriją ir (E)).

Atrodo, jog išvadą išvedėme naudodami tik principus, kurie turėtų būti tapačiai teisingi mūsų modelių teorijoje. Iš tikrųjų klaida susijusi su būtinumo įvedimo pritaikymu formulei (A). Tokiose formulėse kaip (A) laisviems kintamiesiems suteikiame bendrumo interpretaciją⁴: kai (A) pateikiama kaip teorema, – tai suprantama kaip jos paprasto universalaus uždarymo (universal closure) trumpinys

(A′) (y) ((x)A(x) ⊃ A(y))

Jei dabar taikytume būtinumo įvedimo taisyklę formulei (A′), gautume

(B′) ◻(y)((x)A(x) ⊃ A(y)).

Kita vertus, pačią formulę (B) dabar interpretuojame kaip

(B′′) (y)◻((x)A(x) ⊃ A(y)).

Tam, kad išvestume (B′′) iš (B′), mums reikėtų dėsnio, kurio forma būtų ◻(y)C(y) ⊃ (y)◻C(y), o toks dėsnis būtent ir yra Barcan formulės konversija, kurią bandome įrodyti. Iš tikrųjų, galima nesunkiai įsitikinti, kad (B′′) negalioja kontramodelyje, anksčiau pateiktame Barcan schemos konversijai, A(x) pakeitus į P(x).

Tokio keblumo galime išvengti, jei, sekdami Quine’u (1940), savo kvantifikavimo teoriją formuluosime taip, kad tvirtinti bus leidžiama tik uždaras formules. Formulių, turinčių laisvų kintamųjų, tvirtinimas geriausiu atveju aiškinamas patogumo sumetimais – tvirtinimas formulės A(x), kurioje x yra laisvas, visada gali būti pakeistas tvirtinimu formulės (x)A(x).

Jei A yra formulė su laisvais kintamaisiais, tai formulės A uždarymą (closure) apibrėšime kaip bet kokią formulę be laisvų kintamųjų, kuri gaunama prie formulės A prišliejant bendrumo kvantorius ir būtinumo simbolius bet kokia jų eiliškumo tvarka. Tada kvantorinės sistemos M aksiomas apibrėžiame kaip šių schemų uždarymus:

(0) funkcinės teisingumo atžvilgiu tautologijos

(1) ◻ A ⊃ A

(2) ◻ (A ⊃ B) . ⊃ . ◻ A ⊃ ◻ B

(3) A ⊃ (x)A, kai kintamasis x nėra laisvas formulėje A

(4) (x) (A ⊃ B) . ⊃ . (x)A ⊃ (x)B

(5) (y) ((x)A(x) ⊃ A(y))

Išvedimo taisyklė yra materialiosios implikacijos atskyrimo taisyklė. Būtinumo įvedimo taisyklę galima gauti kaip išvestinę.

Norint gauti kvantorinius S4, S5 ar braueriškos sistemos plėtinius reikia prie pateiktų aksiomų schemų tiesiog pridėti visus atitinkamos redukcijos aksiomos uždarymus.

Gautos sistemos pasižymi šiomis savybėmis: jos yra tiesioginiai modalinių teiginių logikų plėtiniai, be modifikacijų, kurių reikalauja Prioro sistema Q; jose substitucijos taisyklė galioja be apribojimų, skirtingai nei Hintikkos išdėstyme; nepaisant to, nei Barcan formulė, nei jos konversija nėra išvedama. Be to, visi kvantifikavimo teorijos dėsniai – modifikuoti, kad būtų suderinami su tuščia sritimi – galioja. Anksčiau pateikta modalinės teiginių logikos semantinio pilnumo teorema gali būti praplėsta ir naujoms sistemoms.

Panorėję galime esamoje sistemoje įvesti egzistavimą kaip predikatą. Semantiniu požiūriu egzistavimas yra vienvietis predikatas E(x), kuris kiekviename m. s. (G, K, R) modelyje φ, kiekviename pasaulyje H ∊ K tenkina tapatybę φ(E, H) = ψ(H). Aksiomatiniu požiūriu jį galime įvesti postuluodami formulių, kurių forma (x)A(x) ∧ E(y). ⊃ . A(y) ir (x)E(x), uždarymus. Predikatą P, kuris buvo naudojamas anksčiau pateiktame kontramodelyje Barcan formulės konversijai, galime atpažinti tiesiog kaip egzistavimą. Šis faktas parodo, kuo egzistavimas skiriasi nuo tautologinio predikato A(x) v ~ A(x), net jei ◻(x)E(x) yra įrodoma. Nors formulė (x)◻(A(x) v ~A(x)) yra tapačiai teisinga, formulė (x)◻E(x) tokia nėra: nors būtina, kad kiekvienas objektas egzistuoja, iš to neplaukia, kad kiekvienas objektas pasižymi savybe būtinai egzistuoti.

Tapatybę galime semantiškai įvesti į modelių teoriją apibrėždami, kad x = y yra teisinga pasaulyje H, kai x ir y yra priskirta ta pati reikšmė, ir klaidinga priešingu atveju. Tada egzistavimas gali būti apibrėžtas per tapatybę, nustatant, kad E(x) reiškia (∃y) (x = y). Platesnė tapatybės teorija dėl čia nedėstomų priežasčių gali būti sukurta priimant sudėtingesnę kvantorinės modelių struktūros sampratą.

Užbaigsime keletu glaustų ir neišbaigtų pastabų apie modalinės logikos „įrodomumo“ interpretacijas, kurias pateiksime tik teiginių skaičiavimui. Jei skaitytojas nuspręstų praleisti šią dalį, jis jau susipažino su pagrindiniu šio straipsnio turiniu. Įrodomumo interpretacijos remiasi pageidavimu formalią sistemą, tarkime, Peano aritmetiką, papildyti būtinumo operatoriumi taip, kad bet kokiai tos sistemos formulei A, ◻A būtų interpretuojama kaip teisinga, jei ir tik jei A yra įrodoma toje sistemoje. Nors buvo argumentuojama, kad tokios modalinio operatoriaus „įrodomumo“ interpretacijos galima atsisakyti vietoje to įvedant įrodomumo predikatą, šliejamą prie formulės A Gödelio numerio, vis dėlto profesoriaus Montague straipsnis šiame tome leidžia bent iš dalies suabejoti tokiu požiūriu.

Aptarkime formalią Peano aritmetikos sistemą PA remdamiesi Kleene’io (1952) formalizacija. Prie formulių sudarymo taisyklių (formation rules) pridedame operatorius ∧, ~ ir ◻ (čia pridedami konjunkcija ir neigimas turi skirtis nuo tų, kurie buvo pradinėje sistemoje), kurie taikomi tik uždaroms formulėms. Modelių teorijoje, kurią pateikėme anksčiau, atominėmis formulėmis laikėme teiginių kintamuosius ir predikatines raides kartu su apskliaustais individiniais kintamaisiais. Čia jomis laikysime tiesiog uždaras taisyklingai sudarytas PA formules (t. y. ne vien tik atomines PA formules). Apibrėžiame modelio struktūrą (G, K, R), kur K – aibė visų netapačių (t. y. neizomorfiškų) skaičių̃ PA modelių, G – standartinis modelis, išreikštas natūraliaisiais skaičiais, o R – dekartiška sandauga K². Apibrėžiame modelį φ reikalaudami, kad bet kokiai atominei formulei P ir H ∊ K, φ(P, H) = T (F), jei ir tik jei P yra teisinga (klaidinga) modelyje H. (Atminkime, kad P yra taisyklingai sudaryta PA formulė, o H yra skaitùs PA modelis.) Sudėtinių formulių vertinimą konstruojame kaip anksčiau⁵. Sakyti, kad A yra teisinga, reiškia sakyti, kad A yra teisinga tikrajame pasaulyje G; o bet kokiai atominei formulei P, φ(◻P, G) = T, jei ir tik jei P yra įrodoma PA sistemoje. (Pastebėtina, kad φ(P, G) = T, jei ir tik jei P yra teisinga intuityvia prasme.) Kadangi (G, K, R) yra S5-m. s., šioje interpretacijoje visi S5 dėsniai yra tapačiai teisingi, ir galėtume parodyti, kad tapačiai teisingi yra tik S5 dėsniai. (Pavyzdžiui, jei P yra Gödelio neišsprendžiama formulė, tai φ(◻P v ◻~P, G) = F, o tai yra kontrapavyzdys „dėsniui“ ◻A v ◻~A.)

Dar viena įrodomumo interpretacija yra tokia: atominėmis formulėmis vėl laikysime uždaras taisyklingai sudarytas PA formules, o naujas formules konstruosime pasitelkdami jungtis ∧, ~ ir ◻. Tarkime, kad K bus aibė visų sutvarkytų porų (E, α), kur E – tai neprieštaringas PA plėtinys, o α – tai (skaitùs) sistemos E modelis. Tarkime, kad G = (PA, α₀), kur α₀ yra standartinis PA modelis. Sakome, kad (E, α) R (E′, α′), kur (E, α) ir (E′, α′) yra aibėje K, jei ir tik jei E′ yra E plėtinys. Atominei P apibrėžiame φ(P, (E, α)) = T (F), jei ir tik jei P yra teisinga (klaidinga) modelyje α. Galime parodyti, kad atominei P φ(◻P, (E, α)) = T, jei ir tik jei P yra įrodoma sistemoje E; o konkrečiu atveju φ(◻P, G) = T, jei ir tik jei P yra įrodoma sistemoje PA. Kadangi (G, K, R) yra S4-m. s., lieka galioti visi S4 dėsniai. Tačiau galioja ne visi S5 dėsniai: jei P yra Gödelio neišsprendžiama formulė, tai φ(~◻P ⊃ ◻~◻P, G) = F. Bet taip pat esama tapačiai teisingų dėsnių, kurie nėra įrodomi sistemoje S4. Pavyzdžiui, bet kokiai A galime įrodyti, kad φ(◻~◻(◊A ∧ ◊~A, G) = T, o iš jo gauti McKinsey’io S4.1 (plg. McKinsey 1945) sistemos teoremas. Šį sunkumą galima būtų pašalinti tam tinkamais pakeitimais, bet čia į tai nesileisime.

Būtų galima suformuluoti panašias M ir braueriškos sistemos interpretacijas. Bet, šio straipsnio autoriaus nuomone, jos yra mažiau įdomios nei tos, kurias jau pateikėme anksčiau. Paminėsime dar vieną klasę įrodomumo interpretacijų – „refleksyvius“ PA plėtinius. Tegu E bus formali sistema, apimanti PA, kurios taisyklingai sudarytos formulės sudaromos iš uždarų PA formulių naudojant jungtis &, ¬ ir ◻ (sakau „&“ ir „¬“ norėdamas pabrėžti, kad naudoju tą pačią konjunkciją ir tą patį neigimą, koks yra pačioje PA, o ne įvedinėju naujus. Žr. išn. 5, p. 152). Tada E vadinama refleksyviu PA plėtiniu, jei ir tik jei: (1) E yra neesminis PA plėtinys; (2) ◻A yra įrodoma sistemoje E, jei ir tik jei įrodoma A; (3) egzistuoja įvertinimas (valuation) α, uždaroms E formulėms priskiriantis reikšmes iš aibės {T, F}, taip, kad konjunkcija ir neigimas veikia pagal įprastas teisingumo lenteles, visos teisingos uždaros PA formulės įgyja reikšmę T, α(◻A) = T, jei ir tik jei A yra įrodoma E, o visos E teoremos įgyja reikšmę T. Įmanoma parodyti, kad esama refleksyvių PA plėtinių, apimančių S4 ir net S4.1 aksiomas, tačiau nėra tokių, kurie apimtų S5 aksiomas.

Galiausiai, pažymime, kad, naudojant įprastą intuicionistinės logikos atvaizdavimą (mapping) S4 sistemoje, galima gauti modelių teoriją intuicionistiniam predikatų skaičiavimui. Čia šios modelių teorijos nepateiksime, bet vietoje to paminėsime vien tik propoziciniam skaičiavimui tam tikrą naudingą intuicionistinės logikos interpretaciją, kylančią iš modelių teorijos. Tarkime, kad E yra bet koks neprieštaringas PA plėtinys. Sakome, kad PA formulė P yra verifikuota sistemoje E, jei ir tik jei P yra įrodoma sistemoje E. Uždaras taisyklingai sudarytas PA formules P laikome atominėmis ir iš jų sudarome formules naudodami intuicionistines jungtis ∧, ∨, ¬ ir ⊃. Tada induktyviai apibrėžiame: A ∧ B yra verifikuota sistemoje E, jei ir tik jei verifikuotos A ir B; A ∨ B yra verifikuota sistemoje E, jei ir tik jei verifikuota A arba B; ¬A yra verifikuota sistemoje E, jei ir tik jei nėra neprieštaringo E plėtinio, kuris verifikuotų A; A ⊃ B yra verifikuota sistemoje E, jei ir tik jei kiekvienas neprieštaringas E plėtinys E′, kuris verifikuoja A, taip pat verifikuoja ir B.

Tada kiekvienas intuicionistinės logikos dėsnio atvejis yra verifikuotas sistemoje PA. Bet, pavyzdžiui, A v ¬A nėra verifikuota, kai A yra Gödelio neišsprendžiama formulė. Tolesniuose darbuose labiau išplėsime šią interpretaciją ir parodysime, kad ją pasitelkdami galime surasti interpretaciją Kreiselio absoliučiai laisvo rinkimo sekų sistemai FC (Kreisel’s system FC of absolutely free choice sequences) (plg. 1958). Beje, akivaizdu, kad S4 ir S5 įrodomumo interpretacijose PA galima pakeisti bet kokia kita teisingumo atžvilgiu funkcine sistema (t. y. bet kokia sistema, kurios modeliai apibrėžia kiekvieną uždarą formulę kaip teisingą arba klaidingą); o intuicionizmo interpretacija gali būti pritaikyta visiškai bet kokiai formaliai sistemai.

Nuorodos

Frege, G., 1892. Über Sinn und Bedeutung. Zeitschrift für Philosophie und philosophische Kritik 100: 25–50. English translations in P. Geach and M. Black, Translations from the Philosophical Writings of Gottlob Frege, Basil Blackwell, Oxford, 1952, and in H. Feigl and W. Sellars (eds.), Readings in Philosophical Analysis, Appleton-Century-Crofts, Inc., New York, 1949.

Hintikka, J., 1959. Existential Pressuposition and Existential Commitments. The Journal of Philosophy 56: 125–137.

Hintikka, J., 1961. Modality and Quantification. Theoria (Lund) 27: 119–128.

Kleene, S. C., 1952. Introduction to Metamathematics. D. Van Nostrand: New York.

Kreisel, G., 1958. A Remark on Free Choice Sequences and the Topological Completeness Proofs. The Journal of Symbolic Logic 23: 369–388.

Kripke, S. A., 1959a. A Completeness Theorem in Modal Logic. The Journal of Symbolic Logic 24: 1–15.

Kripke, S. A., 1959b. Semantical Analysis of Modal Logic (abstract). The Journal of Symbolic Logic 24: 323–324.

Kripke, S. A., 1963. Semantical Analysis of Modal Logic I. Zeitschrift für mathematische Logik und Grund­lagen der Mathematik 9: 67–96.

Leblanc, H., Hailperin, T., 1959. Nondesignating Singular Terms. Philosophical Review 68: 239–243.

McKinsey, J. C. C., 1945. On the Syntactical Construction of Systems of Modal Logic. The Journal of Symbolic Logic 10: 83–94.

Prior, A. N., 1956. Modality and Quantification in S5. The Journal of Symbolic Logic 21: 60–62.

Prior, A. N., 1957. Time and Modality. Clarendon Press: Oxford.

Quine, W. V. O., 1940. Mathematical Logic. Harvard University Press: Cambridge, Mass.

Russell, B., 1905. On Denoting. Mind 14: 479–493.

Strawson, P. F., 1950. On Referring. Mind 59: 320–344.