as a 5-adic number will be written as: ...22222222. Problemos ISSN 1392-1126 eISSN 2424-6158
2025, vol. 107, pp. 91–106 DOI: https://doi.org/10.15388/Problemos.2025.107.7
Maksim Zhuk
European Humanities University, Vilnius, Lithuania
maksim.zhuk@ehu.lt
https://ror.org/04ymc4274
Abstract. In this paper, we consider the project of the philosophy of Number proposed by Alain Badiou. In the first part of the work, we discuss the concept of Numbers proposed by Badiou.
We argue that such a construction is limited and cannot cover all the concepts of Number. In our work, we try to show that Badiou’s universal concept of Number is unfeasible. As a theoretical basis, we are using Laruelle’s non-standard program which we shall discuss in the third part. We admit that Laruelle’s criticism lacks analysis of the mathematical content of Badiou’s ontology. For this, we discuss two examples: floating point arithmetic and p-adic numbers. Both are extremely important conceptual number systems, which cannot be accommodated by Badiou’s philosophy.
Keywords: Badiou, philosophy of Number, non-standard philosophy, Laruelle, p-adic.
Santrauka. Straipsnyje svarstomas skaičiaus filosofijos, pasiūlytos Alaino Badiou, projektas. Pirmojoje teksto dalyje aptariama Badiou pasiūlyta skaičių samprata. Teigiama, kad tokia konstrukcija yra ribota ir negali apimti visų skaičiaus konceptų. Šiuo tekstu bandoma parodyti, kad Badiou pasiūlyta universali skaičiaus samprata neatlaiko kritikos. Teoriniais aspektais remiamasi Laruelle sukurta nestandartine programa, kuri aptariama trečiojoje straipsnio dalyje. Pripažįstama, kad Laruelle kritikoje trūksta matematinio Badiou ontologijos turinio analizės. Šiuo tikslu aptariami du pavyzdžiai: slankiojo kablelio aritmetika ir p-adiciniai skaičiai. Abu šie aspektai yra itin svarbios konceptualiosios skaičių sistemos, kurių neįmanoma integruoti į Badiou filosofiją.
Pagrindiniai žodžiai: Badiou, skaičiaus filosofija, nestandartinė filosofija, Laruelle, p-adicinis skaičius
___________
Received: 26/11/2024. Accepted: 30/06/2025
Copyright © Maksim Zhuk, 2025. Published by Vilnius University Press.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Badiou’s famous ontological program proposes to consider Being as Multiple (Badiou 2005, 29). The language of Multiple is the Set theory, and so, generally speaking, the language of Being is Mathematics. Badiou provides exposition to his ontological program in his three main works (Badiou 2005), (Badiou 2009), and (Badiou 2022). Being is a Multiple without One: it is a collection of collections based on Void, not ‘something’ but a presentation of structured collections. To be is to belong to some Multiple, which is to belong to Situation. Mathematically, this is expressed with the sign of belonging ∈.
Yet it is not the Situation which is important. It is the Event that reveals truth in a given Situation which is the central part of ontology. An Event happens in four possible domains: art, love, science, and politics. According to Badiou, an Event is a Multiple composed of elements of the Situation and itself (Badiou 2005, 179). It could be expressed by the mathematical formula ex={x∈X, ex}, where X is Situation. As this formula is prohibited in the standard set theory, it shows that the Event is unnatural and unpredictable from the Situation itself.
One small, but nevertheless extremely important aspect of this project, which is often overlooked by researchers, was to define the concept of the number itself. The Number is the name of Multiple, specifically, of ordinal numbers which give order to the universe of all sets.
While there is rather extensive literature discussing different aspects of the main Badiou program, both from the mathematical and philosophical perspectives, the Number theory by Badiou has attracted significantly less attention than other works.
Badiou points out that, although we live in an era where numbers are becoming extremely important in the social and political discourses, we do not have a concept of the number as such (Badiou 2008, 1). This is unfortunate as the Number is the most direct way to describe the Multiple.
As Badiou explains:
If Number is the medium in which Nature, grasped in its being, opens itself to our thought, this is, without doubt — as the order of Numbers testifies — because, in the section it carries out, we find, under the simple form of one and three, that dialectic of the position and of the letter which has been recognised, since Galileo, as the true terrain of materialism. Nature consents to its profusion within the fiction of a writing system; and we must recognise in Number the most inscribed instance of being:
“two fingers snap in the abyss,
in scribblebooks a world rushes up,
this depends on you”. (Badiou 2008, 130)
For this task, Badiou uses a system of the so-called surreal numbers proposed by John Conway. He insists that: “we cannot hope to ‘complete’ the inconsistent domain of Numbers, nor to found, outside Number, a hyper-number which would name the invisible lacune in it [...] All the Numbers are already there” (Badiou 2008, 142–143).
In this work, we shall discuss this proposition made by Badiou for creating a unique definition of the Number. We would be mostly concerned with the mathematical aspect. But our goal is not to find mathematical mistakes. We believe that if any mistake exists, they are amendable. For example, Nirenberg, when discussing his ontology, mentions that sets of the form e={e} are non-well-founded and are not used in math (Nirenberg 2011, 598). This is true if we speak about the usual set theory, but non-well-founded set theories exist as well. Even though it is strange that Badiou never used such a theory instead of ZFC, it does not look as a fatal problem to us. There are other examples of sophisticated mathematical analysis of Badiou’s ontology like (Veilahti 2013).
Another approach, which we find more promising, is based on the idea that the set theory is too weak a system to give any direct conclusions about the social or political reality (Nirenberg 2011, 601–603) or (Bolz 2020). As this kind of criticism was already made before, we do not consider it here, either.
Our main concern is that the ontological scheme proposed by Badiou, in spite of his claims, is not a system of freedom from the ‘slavery of numerical’ which he promises (Badiou 2008, 214). It is a rigid and hierarchical system of exclusion and prohibition. This system cannot give us any unique and universal hierarchical ontological order which Badiou envisions. This critical direction was mainly developed by François Laruelle. Laruelle is well known for his own framework in some way ‘opposite’ to Badiou’s ontology. We believe that the weakest point of Laruelle’s criticism is his disinterest with the mathematical aspects. In our work, we want to show some direct examples of ‘inexhaustibility’ of the number world with provided concepts.
Our key counter-thesis to Badiou’s proposal is as follows:
The system of surreal numbers does not include all the numbers that can be thought of. Multiplicity of Being cannot be exhausted by surreals.
In the first part, we discuss the main ideas of the Number theory by Badiou. Then we will provide examples of important numbers which are not covered by Badiou’s system, thus showing its restrictive and prohibitive character. Then, we will discuss how this can be understood in Laruelle’s theoretical framework.
It is also important to note that other aspects of Badiou’s ontological program, developed in the “Being and Event” books, are beyond the scope of this work.
While Richard Dedekind (Dedekind 1901) successfully introduced the concept of irrational numbers, the attempt to give a definition of the idea of the number in general turned out to be much less successful. Indeed, today, number in mathematics has no definition; instead, specific types of numbers are defined, such as natural numbers ℕ, integers ℤ, rational ℚ, real ℝ, and other numbers.
Badiou in his work (Badiou 2008) stated his goal to define what numbers are in general. This definition should cover all possible diversity of the numerical world. Thus, every number that we can think about must be part of this definition and take its place within some well-defined hierarchy. Badiou examines the four classical approaches proposed by Cantor, Peano, Dedekind, and Frege, but rejects them as untenable. According to Badiou, none of these authors was able to present a unified concept that would describe the number as such (Badiou 2008, 10).
Badiou bases his own project on John Conway’s work on surreal numbers. Badiou calls surreal numbers simply Numbers (with the capitalized N) and suggests discarding the term ‘surreal’, which he criticizes. It should be noted that Conway himself, due to the generality of the construction, called surreals simply ‘numbers’. Badiou probably mistakenly believed that the name ‘surreal’ goes back to Conway (Badiou 2008:107); however, it was actually introduced by Donald Knuth in his classic book (Knuth 2011).
Badiou’s construction of surreal numbers differs from that proposed by Conway and Knuth. He starts with the definition of Ordinal numbers. Ordinal numbers by their nature are an ontological scheme of the natural plural (Badiou 2008, 83). Number, as Badiou points out, “[...] is the medium in which Nature, grasped in its being, opens itself to our thought [...]” (Badiou 2008, 130). The beginning of the ordinals is Void, i.e., it is an empty set {}, 0, ∅ (Badiou 2008, 83). In this sense, Void, being a Multiple, is thus in full accordance with the philosophy of Being as a pure multiple (plurality without one). We can get all the natural numbers or ordinals as a composition of multiple Void: ∅, {∅}, {∅ , {∅}. . . Each subsequent ordinal includes the previous one 0 ∈ 1 ∈ 2 ∈3 . . . The ordinals thus have a strict hierarchy.
This order, however, does not simply repeat the familiar idea of natural numbers in a slightly more complex form, but rather allows us to establish a hierarchy beyond the finite. Following the entire collection of finite ordinals 0, 1, 2, 3…, there is a limit ordinal ω – the composition of all finite ordinals. Of course, we can establish its existence only if we initially believe that the infinite exists (Badiou 2008, 82).
We can easily continue the sequence. Beyond the limiting ordinal ω follows: ω + 1, ω + 2, . . ., and so on. And then, again and again, each new sequence generates new limit ordinals that overcome a new infinity. Ordinals order all sets, but, at the same time, they themselves cannot be entirely conceived as a complete One (i.e., there cannot be a set of all ordinals, just as there cannot be a set of all sets). The One of all ordinals is contradictory, because ordinals are pure multiplicity, pure being qua being (Badiou 2008, 139–140).
This, however, is still not enough to obtain all the numbers. Such a sequence does not cover the real numbers, negative or rational. Badiou further gives a general definition: “A Number is conjoint giveness of an ordinal and a part of that ordinal” (Badiou 2008, 102).
Thus, the Number (in general) is an ordinal and some subset of this ordinal. Badiou uses Aristotelian terminology here, by calling the ordinal matter and the indicated subset form. For example, there is a Number consisting of matter {∅} and form ∅. It should be noted that the matter is always an ordinal, but the form is not necessarily an ordinal, although it is always composed of ordinals. The ordinals themselves can also be represented as Numbers, whose form and matter coincide (Badiou 2008, 164).
In order for Numbers to be able to perform the role of the ‘familiar’ numbers, it is necessary to establish how they differ from each other, to indicate the order of the Numbers (and to show that it is identical to the order of familiar numbers), and, of course, to determine the rules of mathematical operations. In this way, one can ‘recognize’ ordinary numbers behind the cumbersome notations, for example, the Number whose matter and form is ∅ is 0.
It can be shown that all the numbers we are familiar with, including negative numbers, rational fractions, and real numbers, exist in this order (Badiou 2008, 177). This is radically different from the classical constructions; for example, according to Dedekind, where real numbers are created after rational numbers, which, in turn, are created from integers: new numbers arise when they are needed, as a superstructure over the already existing ones. According to Badiou, these numbers already exist together and are on an equal basis with all the others (Badiou 2008, 176). However, Numbers give us much more. They extend far beyond the finite, both in the small and large, beyond the limits of the real numbers. It can be shown that Numbers also include infinitesimals. Near each number there are infinitely many infinitesimals. Classical mathematics does not include such numbers. For Badiou, this means the unification of all numbers in a single Multiple being (Badiou 2008, 200). Ultimately, according to Badiou, a number is a Being conceivable in order (Badiou 2008, 211).
The construction of surreal numbers by Conway or Knuth differs from this method, although they result in identical systems. Badiou first constructs ordinals from which he then creates all other Numbers at once and then proves that ordinals can also be considered Numbers. Conway (and Knuth) do not require any special class of numbers to begin the creation of surreal numbers. Conway was critical of a method that would require pre-creation of ordinals (Conway 2000, 226). All that is needed is the following definition: “If L, R are any two sets of numbers, and no members of L is ≥ any member of R, then there is a number {L|R}” (Conway 2000: 4).
It may seem that this definition also requires preliminary preparation (for example, the creation of L and R), but this is not so. This definition does not require the statement that ordinals exist. However, unlike Badiou’s construction, numbers are not created all at once; they are created sequentially, day after day.
On the first day there are no numbers, there is nothing. We can write this as {|}. Despite the fact that we are dealing with nothingness or emptiness, we can see that {|} corresponds to the definition and therefore is a number. We can denote this number in any way, but, for simplicity and convenience, we will choose the sign ‘0’.
On the second day, having a number {|}, which we agreed to denote 01, we can create new objects: {|0}, {0|}, {0|0}. By definition, only the first two are numbers. These are -1 and 1, respectively.
We can continue this creation ad infinitum by creating more and more new numbers every day (we also get objects that are not numbers, as well as repetitions). In a finite number of days, many fractions and integers can be created. However, we can continue creating numbers post infinitum. Real numbers will only be created on the first infinite day of Omega. Of course, we can move on and continue to create different numbers after Omega-day. Conway described this as the process of creating the Universe from Nothing (Conway 2000, 225).
Surreal numbers, which are much more numerous than real numbers, also have ‘holes’ that can be made into some new objects (Conway 2000, 37). Some of these new objects turn out to be quite important. Conway gave names to some of them, such as ∞, which denotes the gap between the real and the positive infinite numbers. However, the collection of gaps is too large to form even a class and cannot exist in some set theories (Conway 2000, 38).
For Conway, numbers are also part of a more general class of objects. As we saw in Conway’s definition, Numbers must consist of two classes, with all elements of the right one strictly greater than all elements of the left one. If we abandon this requirement, then we will get objects called Games. Games differ from Numbers in that some games are not comparable to each other. If any Number is greater, less or equal than another, then the Games can be neither greater, nor less, nor equal. All surreal numbers are games, but not all games are surreal numbers.
There are also other ways to construct surreal numbers (Univalent Foundations Program 2013, 407–419).
From the examples we see that surreal numbers require at least two conditions: adherence to order and belief in the infinite. Next, we will look at some alternative worlds that exist outside of Badiou’s surreal numbers. We could look at many examples, but we will point out only two in which one of Badiou’s requirements are not met: the infinity or order is absent.
In the world of digital technology, many different systems have been implemented that allow computers to calculate; however, one of the most commonly used number systems is the IEEE 754 floating point arithmetic standard (Muller 2009, 3). IEEE 754 is a simulation of the infinite continuous world of real numbers with finite. It is worth noting that we ourselves, finite beings, are no more capable of coming into contact with the infinity of the real line than our computers. The ease with which we designate the infinite makes us forget that we are dealing only with symbols, and not with infinity itself. And not only infinite, but almost all finite numbers are inaccessible to us. In scientific computing or practical problems, where one has to work with something large or small (compared to the normal scales of our everyday life), various forms of floating point arithmetic have been used historically that predate modern standards. Knuth points out that one of the first uses of such a system can be considered Babylonian mathematics. Some other examples could be found in the works of Apollonius. Different methods have been used starting from the 17th century, and they gained widespread importance in the first digital computers (Knuth 1981, 225).
We do not have the opportunity to describe in detail the structure of the IEEE 754 system; we will only point out that its properties are very different from the familiar system of real numbers. In addition to many familiar numbers, IEEE 754 also includes a NaN object – not a number – which allows to close this system relative to the main arithmetic operations. In addition, IEEE 754 includes two infinities –∞ and ∞ (Muller 2009, 20). ‘Ordinary’ finite numbers are divided into two sets with special properties: normal and subnormal numbers. While, the real line has exceptionally good properties:
commutativity a + b = b + a, a * b = b * a,
associativity (a + b) + c = a + (b + c), (a * b) * c = a * (b * c),
and distributiveness a * (b + c) = a * b + a * c,
IEEE 754 preserves commutative operations, but associativity and distributivity are not always satisfied (Muller 2009, 27).
Although IEEE 754 does not contain many of the numbers we are familiar with, and in many cases produces calculations that have results which are different from those expected (or simply wrong), it is one of the foundations of our post-industrial world. In many ways, this strange, finite system, unlike the usual mathematics of the infinite, is much more important than the system of surreal numbers which are beyond any practical applicability today.
The traditional expanding sequence of various classes of numbers is ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ. One of the most difficult steps was the transition from rational to real numbers. Although reals have been known since antiquity, until the 19th century they remained poorly understood.
Real numbers are the basis of our mathematical world, and they play a key role in analysis. The world of real numbers is a world of continuous change and order, where any two numbers are comparable. This order is determined by some absolute value function that allows to measure distances or proximity between numbers2. An absolute value must satisfy the following requirements:
|x| = 0 ⟺ x = 0
|xy| = |x||y|
|x + y| ≤ |x| + |y|
(Gouvea 2020, 31–32).
There are various absolute value functions, however, only three types are known to be applied to the field ℚ:
1. Trivial;
2. Usual absolute value;
3. The absolute value of p-adic value, which has an interesting property
|x + y| ≤ max {|x|, |y|}, i.e., the absolute value of the sum is less than or equal to the maximum of the absolute values.
Those with this last property are called non-Archimedean3, and the spaces created on their basis are ultrametric.
The use of an absolute value or metric allows us to complete rational numbers, to ‘close’ all the ‘holes’ or gaps in it, which allows us to work with methods of mathematical analysis and calculus.
An alternative to the standard absolute value is the p-adic value which measures the magnitude of a number by how well it is divided by some chosen prime number p. That is, the greater the power of p that divides a given number, the smaller it is. This means that, in a 3-adic world, 9 is closer to 3 than, say, 4, and 27 is closer than 9. By using the chosen absolute value, we can create for each chosen prime number an alternative reality to the real numbers:
ℕ ⊂ ℤ ⊂ ℚ ⊂ ℚp ⊂ ℂp
Adic numbers can be written in different ways, one of which is to represent them as an infinite sequence of numbers extending to the left (as opposed to real numbers, which extend to the right). Since adic numbers do not have an order like real numbers, they are neither positive nor negative, which means that the minus sign is not needed.
For example, as a 5-adic number will be written as: ...22222222.
The convenience of this form of notation is that we can use standard school multiplication and addition (while taking into account the use of a non-decimal notation system). If we want to add, say, the number ...222222223, then, remembering that in the 5-digit number system, 5 is written as 10, we get the following:
. . . 222222223
+ . . . 2222222
= . . . 0000000
which is quite natural, since ...2222223 is 1/2.
The p-adic universe(s) has different unusual effects. The p-adic world (or, more precisely, the infinite number of worlds for each prime number) is significantly different from the Reals we are accustomed to. It is well known, for example, that, among 
, there are no square roots of negative numbers. This is, however, not always the case for adic numbers. For example, the square root of -1 in 5-adic would be ...40423140223032431212. By performing ordinary multiplication, one can easily verify that the result ...444444 is indeed -1.
The world of real numbers is well known to us for its clear visual representation in the form of an infinite straight line
The infinite line has a simple linear order, which fascinated Badiou so much that he even demanded the exclusion of complex numbers from the numbers because of their disorder. The complex numbers that form the familiar Euclidean plane, however, present a much clearer and more intuitive image in comparison with the world of p-adic ones. For example, p-adic integers ℤp topologically form a closed unit ball centered at 0. Although we cannot imagine the real numbers in their infinite totality, we have a good idea of the line segment shown in Fig.1, which we are able to extrapolate to the small and large in our imagination. The straight line reflects not only the topology of real numbers, but also their metric and order.
A compact connected set can be depicted as a line segment, a discrete set can be depicted as disconnected points, but how can one depict something that is totally disconnected but is not discrete? There are various ways to visualize p-adic numbers, which, however, only cover some of their properties4. For example, we can arrange them to reflect the proximity of elements. In the illustration below for 3-adic numbers, the numbers inside one circle are closer to each other. In the illustration on the right, we depicted 7-adic numbers as a fractal set, again focusing on their proximity5.
Here, we see that, in a 3-adic world, 0 is closer to 3 than 1, and so on. We can depict adic numbers in a slightly different way, by focusing on their topology. In this case, they represent a disjoint union of self-similar sets. However, these images do not reflect the ‘real’ metrics of numbers or their algebraic properties, as is the case with the real line.
|
|
|
The geometry (or topology) of the ultrametric world is also significantly different from what we are used to. All triangles are isosceles. A triangle with three different sides cannot exist. In the p-adic world, there are no circles, although there are disks or balls, i.e., sets of points distant from the selected point x no further than the distance r. These balls – or disks – however, have very unusual properties (Gouvea 2020, 45–46). For example, any point on a ball is its center, and any two balls are either completely separated or completely contained in each other, i.e., there cannot be a situation like that shown in the picture of Fig. 3. There are no curves in the p-adic world, in the sense in which they exist in the geometry we are familiar with (Gouvea 2020, 109).
It may seem that such a number system is a strange quirk of the imagination. What can be measured with such strange numbers as p-adic? Indeed, we are unlikely to find things around that we would need p-adic numbers to count.
Just as infinitesimals do not occur directly in the reality around us, but served as an instrument of analysis and the foundation of modern physics, or imaginary numbers do not measure anything that can be found in everyday life, but at the same time arise in a wide range of various applied and theoretical problems, p-adic numbers find their application in problems of the number theory and physics (Dragovich 2009).
As we can see, there are various alternate realities that allow us to think about the world in different ways, depending on what decisions we have made. On the one hand, IEEE 754 is the world of finite, on the other hand, the worlds ℚp are with an unimaginable infinity of numbers. One world is strictly ordered, forming an ideal straight line stretching to infinity, whereas the other is chaos crumbling into fractal dust. IEEE 754 is closest to our practice, while esoteric ℚp seems as far removed from everyday life as possible.
Decision as the main philosophical principle was studied by François Laruelle, who is also one of Badiou critics. Being/Real is opaque and inseparable, and, in order to think about it we need to make decisions: “at the edge of Being or of the undecidable, which can only be actualized and realized through the supplement of a decision” (Laruelle 2013, 48).
Laruelle’s main project is a program of non-philosophy or non-standard philosophy. While philosophy defines the boundaries of its tolerance, non-philosophy, like mathematics, has no boundaries. It is the practice of moving forward freely, where new worlds open up that we are free to explore. Of course, historical and social reasons influence the way we structure the world in our minds. We decide to call some things numbers, while others that are similar in many ways are not. What matters is that mathematical truth is not the truth of an authoritarian regime, it is a truth that allows us to make a free choice and take responsibility for it. Non-philosophy refuses philosophical decision and division by accepting a superposition of possibilities (Laruelle 2013, 5). On the other hand, Badiou’s approach, according to Laruelle, is anti-democratic and aristocratic (Laruelle 2013, 35).
François Laruelle writes: “[H]e [Alain Badiou] pursues the project of the re-education of philosophy through mathematics, and not at all that of the constitution of a mathematically based science of philosophy (supposing such a thing were possible)” (Laruelle 2013, vii).
Badiou points out that his approach protects against the anarchy and arbitrariness of capitalism in our world, where everything is counted by number. But, instead, he offers the order of Maoism: a world of ordered thoughts. Each number finds its place in this scheme, as Badiou points out, but what does not find its place in this structure is excluded. The history of the 20th century, as well as the history of Legalism that Badiou writes about (Badiou 2009), contains very tragic examples of how the exclusion of ideas was transformed into the exclusion of subjects.
Badiou easily discards what is not included in the Procrustean (albeit infinite) bed of the surreal number. For example, he points out that complex numbers and quaternions are not numbers, but only superstructures over numbers (Badiou 2008, 228). This is a statement that is unlikely to be accepted by any mathematician or just a person who has become acquainted with the beautiful theory of complex analysis. If complex numbers are not numbers, then equations of the form x2 = –5 have no solution, the fundamental theorem of algebra fails, and so on. We have to work with two types of objects: numbers and ‘constructions’.
In the world of numbers, we simultaneously accept the truth of the existence of real numbers and p-adic, complex and dual. We do not need, as Badiou does, to delineate the boundary and figure out which of these are truly numbers. Badiou, despite using mathematics of the second half of the 20th century, including the category theory, ordinals, remains a supporter of Hilbert’s mathematics, the mathematics of the absolute truth, with his famous aphorism “wir musse wissen, wir wurde wissen”. Badiou, however, prefers to use this maxim as expressed by Mao Tse Tung: “We will come to know everything that we did not know before” (Badiou 2009, 8). It is no coincidence that Badiou showed some appreciation to the ancient Chinese legalists. This is a directive aimed at obtaining the only correct answer. There is one truth (although it may appear in different guises in different worlds), and only the one who is committed to the truth is a Subject.
As Laruelle points out, this is “Plato revisited via Dao and Mao rather than Aristotle, a combination at once conservative and mandarin in spirit” (Laruelle 2013, 36). From the point of view of a non-philosophical approach, this problem is one of philosophy in general: “Its objective is to capture everything under its own authority – its definitions of reality, knowledge, and, most particularly, thinking itself – an aristocratism of thinking” (Maoilearca 2015).
Hilbert in mathematics (like Mao in politics) dreamed of finding a tool for achieving the absolute truth. An algorithmic procedure will reveal all true knowledge. Mathematics, however, has discovered something completely new: truth cannot be discovered algorithmically (Lucas 1961). This does not, in principle, contradict Badiou. On the contrary, since truth cannot be grasped mechanically, then truth can only be revealed to the subject.
However, the fundamental problem is that not only do we not have an algorithm for searching for truth, but we can choose to adhere to different truths, and these truths are not simply linguistic expressions of the same idea, but are generally incompatible. Within a given situation, determined by the logic of the world, the subject is able to discover for oneself various (numerical) worlds that absolutely contradict each other. Berkeley was absolutely right when he pointed out the inconsistency of infinitesimals (they do not exist in ℝ), but Leibniz was absolutely right when he used infinitesimals (they exist in ℝ*). The mathematician and linguist Uspensky noted:
Perhaps in many cases it is generally inappropriate to ask which of a given set of mathematical models best describes physical reality. Apparently, it is reasonable to accept the principle of multiplicity of models and consider that reality is described at once by a whole set of mathematical models that partially contradict each other. (Uspenskij 1987, 119; translated by M.Z.)
Badiou, however, imposes a normative restriction on language, demanding that it be stated as truth that a number is only and exactly a surreal number, but, in this way, we risk losing the opportunity or right to speak about another truth. We are faced with the need to limit thinking only to a certain class of objects. Thus, Badiou demands a hierarchy of order, where the number serves as a means of numbering Being (Laruelle 2013, 34). According to Laruelle, Badiou’s universe is a vertical hierarchy of strictly accounted levels. There are too many of these levels, many more than can be described even with the help of surreal numbers. As soon as our thought has reached the ‘borders’ of the numerical world, we immediately find the opportunity to move on. Conway’s numbers are running out, but they are only a small part of the world of games. Can we move on? It depends on which axioms we accept, or which we reject. For modern mathematics, it is natural to talk about things whose existence has not been proven, and may even be contradictory6.
Historically, the expansion of the numerical reality initially followed the path of expanding our capabilities for understanding the multiplicity of Being. Initially, purely algebraic manipulations encountered obstacles. So, natural numbers were expanded to integers, which allowed us to always subtract, then, fractions appeared, which allowed us to always divide (except for the division by 0). Integers and rational numbers, however, are not closed with respect to the operations of analysis.
In order to close the known rational numbers with respect to mathematical analysis, their field must be supplemented with the real numbers. This operation can be performed in different ways, one of which is Dedekind’s sections. By cutting rational numbers into two classes, we get ‘holes’. These gaps, which are much more numerous than the rational numbers, are the irrational numbers, such as π,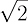 
and others. If we supplement reals with the complex numbers, we close them with respect to all important algebraic operations. As we have already indicated in the ways of completing the rational numbers, we can choose an alternative option, and, instead of ℝ, discover the world of ℚp, which was done at the end of the 19th century. At each of these stages, new opportunities or perspectives arise before us. At every step we make a choice, by accepting what we believe or what we want to follow. We could believe in infinity, we could accept order, or we believe that there is 
.
Alternative (parallel?) worlds of complex numbers are dual and hyperbolic numbers. If, in the world of complex numbers, we have an imaginary unit i2 = –1, then, in the world of duals and hyperbolics, ε2 = 0 and j2 = 1, respectively.
Due to the closure of complex numbers relative to the basic operations of analysis and algebra, further expansion of the numerical world occurred for other reasons. Hamilton constructed the four-dimensional quaternion numbers. Hamilton initially tried to create some kind of an analogue of complex numbers for our three-dimensional space, but objects of this kind did not have some of the good properties of the ‘familiar’ numbers. The vectors were developed in the 19th century, which made it possible to extend mathematization to 3-dimensional space (and a space of any dimension); they were not called numbers, unlike quaternions and octonions.
Historically, mathematical analysis was built by using infinitesimals. However, they are absent in ℝ or ℂ. By abandoning Archimedes’ axiom7, we can create the number line with infinitesimals. Among Numbers, as we have mentioned above, there are both infinitesimal and infinitely large numbers. It may seem that this improves our analytical capabilities compared to ordinary reals, but this is not the case. Analysis in Numbers is still in its infancy.
However, we can again make a different choice and discover another world unlike the world of surreal numbers – these are infinitesimals of smooth infinitesimal analysis (SIA). In this case, we will be forced to abandon classical logic and, instead, accept the logic of intuitionistic mathematics. In particular, we are losing the law of excluded middle. By abandoning this convenient principle, we can construct the ‘smooth world’ 
. We get an infinitesimal neighborhood of 0, consisting of points of elements indistinguishable from 0, about which we, however, cannot say that they are equal to 0 (Bell 2008, 6). Such numbers are infinitesimals, and, in a sense, they exist virtually (Bell 2008, 7). The only infinitesimal that we can ‘show’ is 0. All the others disappear after calculations. Due to this, each point on a smooth curve ‘looks like’, as it has, a small straight segment around (Bell 2008, 9). Koch put it this way: such a segment is so small that one cannot distinguish the graph of a function from a segment of a straight line, but is big enough that its slope is uniquely determined (Lavendhomme 1996, 2). Functions defined everywhere on ℝ are everywhere continuous and infinitely differentiable (Lavendhomme 1996, 1).
In this way, it becomes possible to make mathematical analysis in an algebraic way, to explain the mysterious operations with infinitesimals that caused difficulties for Leibniz and other mathematicians and became the object of Berkeley’s criticism, and to construct differential geometry synthetically.
If we abandon the certainty and precision of the operation of belonging to a set, we can get the so-called fuzzy numbers, and so on.
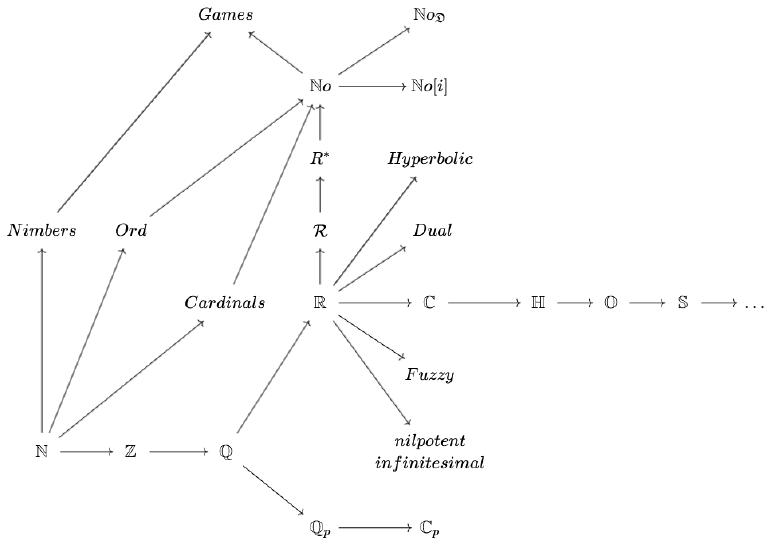
In Fig. 4, we can see some (far from exhaustive) the relations of objects which are usually called numbers. At each possible branch of this scheme, we can make a new choice, make a decision that has some consequences, for example, to engage in analysis in the world of hyperreal or nilpotent numbers, or to abandon infinitesimals altogether, by choosing the classical approach of limits. Mathematics is thus a free activity in which we can apply different ways of thinking. We are free to think about things (how to count things in this case) as we wish, as long as our thoughts remain clear.
Badiou’s Multiple without a One is subordinate to a precise hierarchy. Laruelle’s world is an immanent One that can be represented in various ways. Representation creates a vision of Being that stems from how we choose to divide Being in order to make it part of our thought.
In non-philosophy, all thoughts are equalized. However, this equivalence or conceptual democracy is not political in the philosophical and representational sense of the term (with all its attendant troubles). It is not a theoretical democracy – which would leave what counts as ‘theory’ alone – but the ‘democracy of theory itself’. Such a nonrepresentational democracy aims to resolve the traditional hierarchies of philosophy “with experience, art, ethics, technology, mysticism, science, etc.”, by mutating just what thought and theory might be – by “universalizing thought beyond philosophy” (Maoilearca 2015).
Badiou’s ontology is a set of multiple parallel worlds organized around a single truth that can be discovered in each of the worlds. On the other hand, Laruelle’s world is the One, which opens up the possibility of thinking different as equal.
In our work, we have examined the ontology of number proposed by Alain Badiou. Number, through ordinals and cardinals, plays a key role in his metaphysics of Being, described in the work “Being and Event”. Badiou strives to give a precise, unified definition of number that would encompass all of mathematics. We used Laruelle’s criticism to show that Badiou’s approach creates a rigid hierarchy of exclusion and division. By using specific examples, we have demonstrated that the proposed system of surreal numbers does not encompass the total numerical reality, and that it excludes important classes of numbers, such as the number systems of the computer digital world.
For both Laruelle and Badiou, the world is immanent. Truth exists and is revealed by the subject in Badiou’s ontology. In Laruelle’s perception, the subject makes a philosophical decision to separate themselves from Being in order to think it. However, the mathematical procedure allows us to create new thoughts about things that, being a material immanent part of Being, did not exist before: in this way, we ‘expand’ Being: by crossing the border, we each time discover a new world that did not exist before. Thus, although truth is immanent in the world, as Badiou pointed out, the very world in which it is revealed is new. Contradictory truths exist, and anyone can become a subject by committing to a completely different truth about numbers.
Badiou, A., 2008. Number and Numbers. Oxford: Polity Press.
Badiou, A., 2005. Being and Event. Translated by O. Feltham. London: Continuum.
Badiou, A., 2009. Logics of Worlds: Being and Event, 2. Translated by O. Feltham. London: Continuum.
Badiou, A., 2022. The Immanence of Truths: Being and Event III. Translated by K. Reinhard and Susan Spitzer. London: Bloomsbury.
Bell, J., 2008. A Primer of Infinitesimal Analysis. Cambridge: University Press.
Bolz, R., 2020. Mathematics is Ontology? A Critique of Badiou’s Ontological Framing of Set Theory. Filozofski Vestnik 2(41):119–142. https://doi.org/10.3986/fv.41.2.06
Conway, J. H., 2000. On Numbers and Games. Natick, MA: A K Peters/CRC Press.
Cuoco, A. A., 1991. Visualizing the P-Adic Integers. The American Mathematical Monthly 98(4): 355–64. https://doi.org/10.2307/2323809.
Dedekind, R., 1901. Essays on the theory of numbers: I. Continuity and irrational numbers, II. The nature and meaning of numbers. Translated by Wooster Woodruff Beman. Chicago: Open Court Publishing Company.
Dragovich, B., Khrennikov, A.Y., Kozyrev, S.V. et al., 2009. On p-adic Mathematical Physics. P-Adic Numbers, Ultrametric Analysis, and Applications 1, 1–17. https://doi.org/10.1134/S2070046609010014
Gouvea, F. Q., 2020. p-adic Numbers: An Introduction. 3rd ed. Switzerland: Springer Cham. https://doi.org/10.1007/978-3-030-47295-5
Kanamori, A., 2009. The Higher Infinite: Large Cardinals in Set Theory from their Beginnings. New York: Springer. https://doi.org/10.1007/978-3-540-88867-3
Knuth, D. E., 1981. The Art of Computer Programming: Seminumerical Algorithms v. 2. Boston, MA: Addison-Wesley Educational.
Knuth, D. E., 2011. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness; a Mathematical Novelette. Reading, Massachusetts: Addison-Wesley.
Laruelle, F., 2013. Anti-badiou: The Introduction of Maoism into Philosophy. Translated by R. Mackay. New York: Continuum Publishing Corporation.
Lavendhomme, R., 1996. Basic Concepts of Synthetic Differential Geometry. Netherlands: Springer.
Lucas, J. R., 1961. Minds, Machines and Gödel. Philosophy 36(137): 112–127.
Maoilearca, J. O., 2015. All Thoughts are Equal: Laruelle and Nonhuman Philosophy. Minneapolis: University of Minnesota Press.
Muller, J. M. et al., 2009. Handbook of Floating-point Arithmetic. Cambridge: Birkhäuser.
Nirenberg, R. L., and Nirenberg, D., 2011. Badiou’s Number: A Critique of Mathematics as Ontology. Critical Inquiry 37(4): 583–614. https://doi.org/10.1086/660983
Robert, A. M., 2000. A Course in P-Adic Analysis. New York: Springer.
Univalent Foundations Program., 2013. Homotopy Type Theory: Univalent Foundations of Mathematics.
Veilahti, A., 2013. Alain Badiou’s Mistake: Two Postulates of Dialectic Materialism. Available at: https://arxiv.org/abs/1301.1203 (Accessed: 3 July 2025).
Uspenskij, V. A., 1987. Chto Takoe Nestandartnyj Analiz? Moskva: Nauka.
1 At this stage we cannot yet say that this sign really corresponds to the number 0, since we have not determined its properties yet.
2 The absolute value allows us to determine the metric, which, in turn, allows us to determine the topology, i.e., the concept of proximity and connectivity of elements. This is necessary to establish mathematical analysis.
3 Here we should pay attention to two meanings in which the term ‘Archimedean’ is used. We are talking about violation of the triangle inequality.
4 Interesting fractal sets of p-adic numbers can be found in (Robert 2000, 7–17).
5 This illustration is based on (Cuoco 1991).
6 For more details, see (Kanamori 2009).
7 It is important not to confuse it with the Archimedean property that we talked about earlier, although there is a certain connection between them.
