Problemos ISSN 1392-1126 eISSN 2424-6158
2025, vol. 107, pp. 190–206 DOI: https://doi.org/10.15388/Problemos.2025.107.14
Vertimai / Translations
Aktualizmas ir galimi pasauliai
Alvin Plantinga
Kalvino koledžas (JAV)
Iš anglų kalbos vertė ir pratarmę parašė Pranciškus Gricius
(Oksfordo universitetas, Vilniaus universitetas)
Alvino Plantingos (g. 1932) straipsnis, kurio lietuviškas vertimas pristatomas skaitytojui, – tai vienas pirmųjų bandymų suderinti aktualistinę ir kontingentistinę modalinę metafiziką su Saulo Kripkės išplėtota galimų pasaulių semantika. Aktualizmas – tai nuostata, kad nėra ir negalėtų būti neegzistuojančių objektų, o kontingentizmas – tai pažiūra, kad yra ar galėjo būti atsitiktinai egzistuojančių objektų. Įprasta kvantorinės modalinės logikos galimų pasaulių semantika, Plantingos teigimu, yra nesuderinama su aktualizmu ir kontingentizmu. Pagrindinė problema čia ta, kad galimų pasaulių semantikoje numatoma, jog kiekvieno pasaulio kvantifikavimo sritis jau duota. Taigi, jei priimama kontingentistinė nuostata, kad galėjo egzistuoti objektas, kuris faktiškai neegzistuoja, privalu pripažinti, jog egzistuoja nefaktinio pasaulio kvantifikavimo sritis, kurioje yra neegzistuojantis objektas. Vadinasi, esama neegzistuojančių objektų, nes aibės (taigi ir kvantifikavimo sritys) egzistuoja tik jei egzistuoja jų nariai. Teiginys, kad esama neegzistuojančių objektų, prieštarauja aktualistinėms nuostatoms.
Plantinga šią problemą sprendžia trimis žingsniais. Pirma, jis priima nuostatą, kad teiginiai, savybės, ryšiai ir panašios esatys egzistuoja ne atsitiktinai, o būtinai. Antra, tarp šių esačių jis identifikuoja objektų esmes (kur objekto esmė – tai esminė ir būtinai unikali objekto savybė). Trečia, Plantinga pasiūlo alternatyvią kvantorinės modalinės logikos semantiką, kurioje modalinių sakinių teisingumo sąlygos nusakomos nurodant ne objektus, o objektų esmes ir pastarųjų koinstanciaciją su kitomis savybėmis.
Versta iš:
Alvin Plantinga. 1976. Actualism and Possible Worlds.
Theoria 42: 139–160.
___________
Padėka. Dėkoju Alvino Plantingos sūnui Carlui Plantingai, maloniai suteikusiam leidimą išversti ir publikuoti šį tekstą lietuvių kalba. Taip pat nuoširdžiai dėkoju Živilei Pabijutaitei, išvertusiai straipsnyje pasirodančią Boecijaus citatą iš lotyniškojo originalo. Finansavimą skyrė Lietuvos mokslo taryba, sutarties Nr. S-MIP-22-16.
___________
Copyright © Alvin Plantinga. Translation from English to Lithuanian, preface Copyright © Pranciškus Gricius, 2025.
Published by Vilnius University Press. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
___________
Galimų pasaulių idėja žadėjo ir, esu įsitikinęs, suteikė supratimo bei įžvalgų daugybėje temų. Manau, kad svarbiausia iš jų yra loginė galimybė plačiąja prasme – tiek de dicto, tiek de re. Bet esama ir kitų temų: teiginių, savybių ir aibių prigimtis, tikrinių vardų ir apibrėžiamųjų deskripcijų veikimas, kontrafaktinių teiginių prigimtis, laikas ir laikiniai ryšiai, kauzalinis determinizmas, filosofinėje teologijoje – ontologinis įrodymas, teologinis determinizmas ir blogio problema (žr. Plantinga 1974 skyrius IV–X). Visgi, rodos, kad vienu atžvilgiu galimų pasaulių idėja suteikė mažiau aiškumo nei atnešė painiavos, mat rimtai priėmus šią idėją gali tekti įsipareigoti abejotinai minčiai, kad yra ar galėtų būti neegzistuojančių objektų. Leiskite man paaiškinti.
I. Kanoninė galimų pasaulių samprata
Per pastarąjį ketvirtį amžiaus pasirodė nemažai vis įspūdingesnių ir sėkmingesnių bandymų semantiškai suprasti modalinę logiką bei įdomų modalinį natūralios kalbos fragmentą (žr., pavyzdžiui, Kripke 1963; Lewis 1972: 169 ir Montague 1974). Šiuose mėginimuose siūloma tokia galimų pasaulių samprata. Pavadinkime ją kanonine samprata. Patys galimi pasauliai įprastai „priimami kaip baziniai“, bet, aiškinant neformaliai, galima sakyti, jog galimas pasaulis yra būdas, kaip dalykai galėtų būti – visa apimantis būdas. Tarp šių būdų, kaip dalykai galėtų būti, vienas – pavadinkime jį „α“ – išsiskiria tuo, kad yra faktinis: tai būdas, kaip dalykai iš tikrųjų yra. α yra vienintelis galimas pasaulis, kuris galioja ar yra faktinis. Visi kiti yra vien galimi. Su kiekvienu galimu pasauliu susieta aibė individų ar objektų – galimo pasaulio W sritis, kurią galime vadinti „ψ(W)“. Aibės ψ(W) nariai yra objektai, kurie egzistuoja pasaulyje W. Savaime suprantama, skirtingi objektai gali egzistuoti skirtinguose pasauliuose. Kaip sako Kripkė (1963: 65):
Intuityviai ψ(W) yra visų pasaulyje W egzistuojančių individų aibė. Tarp kitko, verta pastebėti, jog skirtingiems argumentams W aibė ψ(W) neturi būti ta pati, lygiai taip, kaip intuityviai kituose nei tikrasis pasauliuose gali nebūti kai kurių faktiškai egzistuojančių individų ir gali atsirasti naujų individų.
Tad kiekvienas galimas pasaulis W turi savo sritį ψ(W). Taip pat esama ir visų pasaulių sričių sąjungos – pavadinkime ją U. Į šią aibę patenka faktiniame pasaulyje α egzistuojantys objektai bei objektai, jei tokių esama, kurie neegzistuoja pasaulyje α, bet kurie egzistuoja kituose galimuose pasauliuose.
Remiantis kanonine samprata, teiginiai laikomi esatimis iš aibių teorijos – galbūt galimų pasaulių aibėmis ar funkcijomis iš pasaulių aibės į teisingumą arba klaidingumą. Jei teiginius laikome pasaulių aibėmis, tai teiginys yra teisingas duotajame pasaulyje W, jei W yra jo narys. Tada būtini teiginiai yra teiginiai, teisingi visuose pasauliuose. Galimi teiginiai yra teisingi bent viename pasaulyje. Neįmanomi teiginiai nėra teisingi nė viename. Dar daugiau, teigiama, kad U nariai turi savybes ar patenka į ryšius galimuose pasauliuose. Savybės ir ryšiai, kaip ir teiginiai, yra esatys iš aibių teorijos: galbūt funkcijos iš galimų pasaulių į aibes sutvarkytų n-viečių aibių, kurių nariai yra iš U. Jei paprastumo dėlei nepaisysime ryšių ir tęsime tik su savybėmis, tai galime nepaisyti sutvarkytų n-viečių aibių ir sakyti, kad savybės yra funkcijos iš pasaulių į aibes U narių. Tada savybė P turi ekstensiją duotajame pasaulyje W: aibę objektų, kuri yra P reikšmė pasaulio W atžvilgiu. Pasaulyje W objektas turi savybę P, jei jis yra P ekstensijoje pasaulio W atžvilgiu. Žinoma, objektas gali turėti skirtingas savybes skirtinguose pasauliuose. Faktiniame pasaulyje W. V. Quine’as yra įžymus filosofas, bet kitame pasaulyje jis šios savybės neturi, o vietoj to jis, tarkime, yra įžymus politikas. Modalines objektų savybes dabar galima aiškinti taip pat, kaip ir modalines teiginių savybes: objektas x turi savybę P atsitiktinai ar kontingentiškai, jei jis turi P, bet neturi P visuose galimuose pasauliuose. Taigi, savybė būti filosofu yra atsitiktinė Quine’ui. Kita vertus, x turi P esmingai ar būtinai, jei x turi P visuose galimuose pasauliuose. Nors būti filosofu yra atsitiktina Quine’ui, būti asmeniu, galbūt, yra jam esminga: galbūt nėra galimo pasaulio, kuriame jis neturi šios savybės.
Duotajame galimame pasaulyje kvantifikuojama to galimo pasaulio sritis. Toks teiginys, kaip
(1) (∃x) x yra violetinė karvė
yra teisingas duotajame pasaulyje W, tik jei pasaulio W sritis ψ(W) įtraukia objektą, kuris pasaulyje W turi savybę būti violetine karve. Kitaip tariant, teiginys (1) yra teisingas pasaulyje W, tik jei yra U narys, kuris yra įtrauktas į būti violetine karve ekstensiją pasaulio W atžvilgiu ir kuris taip pat įtrauktas į ψ(W). Faktas, jei tai faktas, kad kažkoks U narys, neįtrauktas į ψ(W), turi savybę būti violetine karve pasaulyje W, nėra svarbus. Dabar aišku, kaip reikia suprasti tokius teiginius, kaip
(2) ◇(∃x) x yra violetinė karvė
ir
(3) (∃x) ◇ x yra violetinė karvė.
Teiginys (2) yra teisingas, jei yra galimas pasaulis, kuriame teisingas (1). Taigi, jis yra teisingas, jei yra U narys, taip pat esantis ψ(W) nariu kažkuriam pasauliui W, kuriame jis turi savybę būti violetine karve. Kita vertus, teiginys (3) yra teisingas, jei ir tik jei pasaulio α sritis ψ(α) ir faktinis pasaulis įtraukia objektą, kuris kažkuriame pasaulyje W turi savybę būti violetine karve. Taigi, teiginys (2) būtų teisingas, o (3) – klaidingas, jei nė vienas ψ(α) narys nėra violetinė karvė nė viename iš pasaulių, bet kažkuris U narys egzistuoja pasaulyje, kuriame jis yra violetinė karvė. (3) būtų teisingas, o (2) – klaidingas, jei kažkuris ψ(α) narys yra violetinė karvė kažkuriame pasaulyje, bet nė vienas U narys nėra violetinė karvė nė viename pasaulyje, kuriame jis egzistuoja.
Sustokime ir pasidžiaukime neįtikėtinu šios schemos išradingumu. Vis dėlto gyvenimas per trumpas, tad tiesiog paminėkime, kad kanoninė samprata iš tikro yra išradinga ir kad ji tikrai leidžia mums geriau suprasti modalumus. Tačiau manau, kad vienu atžvilgu ji ne suteikia aiškumo, o atneša painiavą: mat ji gali įteigti mintį, kad esama neegzistuojančių objektų. Kaip tiksliau iškyla nemalonus neegzistuojančių objektų klausimas? Žinoma, kanoninė schema pati savaime neteigia, kad esama neegzistuojančių objektų, mat galbūt faktinio pasaulio sritis ψ(α) sutampa su U. Kitaip tariant, pati kanoninė samprata neatmeta idėjos, kad tarp galimų pasaulių esama tokių, kuriuose egzistuoja viskas, kas egzistuoja bent viename iš pasaulių. Ir pati schema nenumato, kad α nėra būtent toks pasaulis. Vis dėlto esama labai tikėtino teiginio, kurio konjunkcija su kanonine samprata implikuoja, kad ψ(α) ≠ U. Tikrai tikėtina tarti, kad galėtų būti objektas, netapatus nė vienam faktiškai egzistuojančiam objektui, t. y.
(4) galimai, yra objektas, netapatus nė vienam pasaulyje α egzistuojančiam objektui.
Jei (4) yra teisingas, tai (remiantis kanonine schema) yra galimas pasaulis W, kuriame egzistuoja objektas, netapatus nė vienam pasaulyje α egzistuojančiam objektui. Taigi, ψ(W) įtraukia objektą, kuris nėra ψ(α) narys. Tad tą patį galima sakyti ir apie U. Vadinasi, U įtraukia objektą, kuris neegzistuoja pasaulyje α. Šis objektas neegzistuoja faktiniame pasaulyje, taigi, jis neegzistuoja. Vadinasi, mes esame įsipareigoję nuostatai, kad esama neegzistuojančių objektų, jei priimame kanoninę sampratą ir numatome, kad galėtų būti objektas, netapatus nė vienam faktiškai egzistuojančiam objektui.
Ir net jei atmestume (4), vis tiek remdamiesi kanonine schema mes būtume įsipareigoję idėjai, kad galėjo būti neegzistuojančių objektų. Juk, žinoma, esama galimų pasaulių, kuriuose aš ir tu neegzistuojame. Šie pasauliai, be abejonės, kur kas prastesni, bet vien dėl to jie nėra neįmanomi. Taigi, yra galimas pasaulis W, kuriame tu ir aš neegzistuojame. Bet tada ψ(W) ≠ U. Taigi, jei W būtų buvęs faktinis, tai visų galimų objektų aibė U būtų turėjusi neegzistuojančių narių – būtų buvę neegzistuojančių objektų. Iš tikrųjų tu ir aš būtume buvę būtent tokie objektai. Taigi, kanoninė galimų pasaulių samprata yra įsipareigojusi idėjai, kad yra ar galėtų būti neegzistuojančių objektų.
II. Aktualisto galimų pasaulių samprata
Sakiau, kad kanoninė galimų pasaulių samprata atneša painiavą neegzistuojančių objektų idėjos atžvilgiu. Taip sakau, kadangi manau, jog nėra ir negalėtų būti neegzistuojančių objektų. Pati neegzistuojančio objekto idėja yra nesusipratimas ar gerų geriausiai – tai sąvoka, kurios instanciacija yra neįmanoma, kaip ir apskrito kvadrato. Vis dėlto dabartiniame kontekste šis pastebėjimas gali užkirsti kelią įdomiems klausimams. Vietoj to geriau sakykime, kad kanoninė galimų pasaulių samprata sumoka nemenką ontologinį mokestį. Jei įžvalgos ir supratimas, kurį ji neginčijamai suteikia, gali būti pasiekti tik mokant tokią kainą, tai mes turime pagrindo sukąsti dantis ir susimokėti arba galbūt turime pagrindo atmesti pačią galimų pasaulių idėją. Vis dėlto aš įrodinėsiu, kad galime gauti visas tas įžvalgas nemokėdami tos kainos. (Jūs galbūt manysite, kad ši taktika turi, kaip mus moko garsioji ištara, visus vagystės pranašumus prieš sąžiningą triūsą (angl. all the advantages of theft over honest toil); jei taip, tai, tikiuosi, jūs klystate). Sekime Robertu Adamsu (1974: 211) ir „aktualizmu“ įvardykime nuostatą, kad nėra ir negalėtų būti neegzistuojančių objektų. Galimi pasauliai kartais stigmatizuojami kaip „neteisėtos neapibrėžtų objektų totalybės“. Žvelgiant iš aktualisto požiūrio taško, ši stigmatizacija išties taikli. Bet mes pabandykime panaikinti šią stigmą. Mes sieksime, išlikdami aktualistais, pasisavinti tai, ką galimų pasaulių schema mums siūlo. Mėginsiu išplėtoti aktualistinę galimų pasaulių sampratą svarstydamas tokias penkias temas:
(1) pasauliai ir knygos,
(2) savybės,
(3) esmė ir α-transformacija,
(4) sritys ir teiginiai
ir
(5) esmės ir teisingumo sąlygos.
1. Pasauliai ir knygos. Pradedame nuo dalykų padėties sąvokos. Manau, kad yra akivaizdu, jog esama dalykų padėčių: pavyzdžiui, Quine’o buvimas įžymiu filosofu. Kiti pavyzdžiai yra Quine’o buvimas įžymiu politiku, 9-nių buvimas pirminiu skaičiumi ir dalykų padėtis, susidedanti iš visų žmonių buvimo mirtingų. Kai kurios dalykų padėtys – pavyzdžiui, Quine’o buvimas filosofu ir 7 + 5 buvimas 12 – galioja arba yra faktinės. O Quine’o buvimas politiku yra dalykų padėtis, kuri nėra faktinė, ji negalioja. Žinoma, neteigiu, kad ši dalykų padėtis neegzistuoja, kad paprasčiausia nėra tokios dalykų padėties. Iš tikrųjų ši dalykų padėtis yra, ji egzistuoja lygiai taip pat, kaip ir bet kuri griežtai faktinė dalykų padėtis. Tačiau ji negalioja, ji nėra faktinė. Vis dėlto ji galėjo būti faktinė, ir jei dalykai būtų susiklostę atitinkamai kitaip, tai ji būtų buvusi faktinė: ji yra galima dalykų padėtis. Kita vertus, 9-nių buvimas pirminiu skaičiumi yra neįmanoma dalykų padėtis, kuri negalioja ir negalėtų galioti.
Galimas pasaulis yra galima dalykų padėtis. Tačiau ne bet kuri galima dalykų padėtis yra galimas pasaulis: tam, kad pasiektų šį statusą, dalykų padėtis turi būti išsami ar maksimali. Šitai mes galime paaiškinti tokiu būdu. Sakykime, kad dalykų padėtis S įtraukia dalykų padėtį S*, jei nėra galima, jog S galiotų, o S* negaliotų. Sakykime, kad S užkerta kelią S*, jei nėra galima, kad jos abi galiotų. Tada maksimali dalykų padėtis yra tokia, kuri arba įtraukia, arba užkerta kelią kiekvienai dalykų padėčiai S. O galimas pasaulis yra dalykų padėtis, kuri yra ir galima, ir maksimali. Lygiai taip pat, kaip ir remiantis kanonine samprata, yra tik vienas galimas pasaulis – α, kuris išsiskiria tuo, kad kiekviena jo įtraukta dalykų padėtis yra faktinė. Taigi, α yra faktinis pasaulis. Visi kiti galėjo būti faktiniai, bet faktiškai tokie nėra. Galimi pasauliai yra dalykų padėtys, taigi jie yra abstraktūs objektai. Taigi, faktinis pasaulis α yra abstraktus objektas. Jis neturi masės centro. Jis nėra nei konkretus objektas, nei konkrečių objektų mereologinė suma. Iš tikrųjų, α, kaip ir Fordo buvimas išradingo, išvis neturi erdvinių dalių. Pastebėkime, kad mes pradėjome nuo dalykų padėčių galimumo ir faktiškumo sąvokų. Priėmę šį galimų pasaulių aiškinimą, mes dabar negalime prasmingai aiškinti galimybės kaip įtraukties į kažkokį galimą pasaulį ar faktiškumo kaip įtraukties į faktinį pasaulį. Aiškinama turi būti atvirkščiai.
Manau, kad taip pat akivaizdu, jog yra tokie dalykai kaip teiginiai – tai dalykai, kurie yra teisingi ar klaidingi, kurie yra manomi, tvirtinami, atmetami, svarstomi ir panašiai. Kad tokie dalykai yra, manau, yra neginčijama. Bet gali kilti klausimų apie jų prigimtį. Galime klausti, pavyzdžiui, ar teiginiai yra sakiniai, ar konkrečios sakinių ištaros, ar ekvivalenčios sakinių klasės, ar kažkokie kitokio pobūdžio dalykai. Mes galime klausti, ar jie yra dalykų padėtys: ar iš tikrųjų yra du skirtingo pobūdžio dalykai – teiginiai ir dalykų padėtys, ar tik vienas? Aš linkstu priimti pirmą požiūrį, kadangi teiginiai turi savybę – teisingumą ir klaidingumą, kurios neturi dalykų padėtys. Bet kuriuo atveju yra teiginiai ir yra dalykų padėtys. Tikiuosi, kad tai, ką toliau teigsiu, bus teisinga, net jei teiginiai ir yra dalykų padėtys.
Galime pritarti kanoninei sampratai ir teigti, kad teiginiai yra teisingi ar klaidingi galimuose pasauliuose. Teiginys p yra teisingas dalykų padėtyje S, jei nėra galima, kad S būtų faktinė ir p būtų klaidingas. Taigi, teiginys
(5) Quine’as yra filosofas
yra teisingas dalykų padėtyje Quine’o buvimas įžymiu filosofu. Tad teiginys p yra teisingas pasaulyje W, jei neįmanoma, kad W galiotų ir p būtų klaidingas. Pasaulyje α teisingi teiginiai, akivaizdu, sutampa su teisingais teiginiais. Žinoma, čia teisingumas yra bazinė sąvoka. Teisingumo nederėtų aiškinti per teisingumą faktiniame pasaulyje ar teisingumą pasaulyje α. Aiškinama atvirkščiai. Pavyzdžiui, teisingumas pasaulyje α turi būti apibrėžtas per teisingumą ir modalines sąvokas. Aibė teiginių, teisingų duotame pasaulyje W, yra pasaulio W knyga. Knygos, kaip ir pasauliai, turi maksimalumo savybę: bet kokiam teiginiui p ir knygai B galioja, kad arba B įtraukia p, arba B įtraukia p neigimą p̄. Faktinio pasaulio α knyga yra aibė teisingų teiginių. Akivaizdu, kad tam tikri teiginiai yra teisingi tik viename pasaulyje. Pavyzdžiui, teiginys
(6) α yra faktinis
yra teisingas pasaulyje α ir tik pasaulyje α. Taigi, jei norime, tai knygą galime laikyti ne teiginių aibe, o teiginiu, kuris yra teisingas tik viename pasaulyje.
2. Savybės. Remiantis kanonine samprata, objektai turi savybes pasauliuose. Kaip aktualistai mes galime pritarti šiam požiūriui: objektas x turi savybę P pasaulyje W, jei ir tik jei nėra galima, kad W būtų faktinis ir x turėtų P neigimą. Vis dėlto esame priversti atmesti kanoninę savybių sampratą. Remiantis šia samprata, savybė yra esatis iš aibių teorijos: galbūt funkcija iš pasaulių į aibes individų. Ši samprata turi du trūkumus. Visų pirma, ji numato, kad nėra netapačių, bet būtinai koekstensyvių savybių, t. y. kad nėra netapačių savybių P ir P*, kurioms galioja, jog nėra galimo pasaulio W, kuriame kažkoks objektas turi P, bet ne P*. Bet, žinoma, esama tokių savybių. Savybė būti 3-jų kvadratu yra būtinai koekstensyvi savybei būti 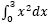 . Bet, žinoma, jos nėra viena ir ta pati savybė. Jei ontologinis įrodymas yra korektiškas, tai savybė žinoti, kad Dievas neegzistuoja, yra būtinai koekstensyvi savybei būti apskritu kvadratu. Bet, žinoma, jos nėra ta pati savybė, net jei tas įrodymas korektiškas.
. Bet, žinoma, jos nėra viena ir ta pati savybė. Jei ontologinis įrodymas yra korektiškas, tai savybė žinoti, kad Dievas neegzistuoja, yra būtinai koekstensyvi savybei būti apskritu kvadratu. Bet, žinoma, jos nėra ta pati savybė, net jei tas įrodymas korektiškas.
Žvelgiant iš aktualisto požiūrio taško, antrasis trūkumas yra svarbesnis. Gana akivaizdu, kad, pavyzdžiui, savybė būti filosofu būtų egzistavusi, net jei vienas objektas, kuris yra filosofu – tarkime, Quine’as – būtų neegzistavęs. Bet dabar apsvarstykime kanoninę sampratą, kuria remiantis būti filosofu yra funkcija iš galimų pasaulių į aibes individų; ši funkcija – tai aibė sutvarkytų porų, kurių pirmieji nariai yra pasauliai ir kurių antrieji nariai yra aibės individų. Šitai nedera su ką tik minėta tiesa. Mat jei Quine’as būtų neegzistavęs, taip pat nebūtų egzistavusios jį turinčios aibės. Pavyzdžiui, vieninė Quine’o aibė negalėtų egzistuoti, jei Quine’as nebūtų egzistavęs. Žvelgiant iš aktualisto požiūrio taško, jei Quine’as nebūtų egzistavęs, tai išvis nebūtų buvę tokio objekto kaip Quine’as, ir tokiu atveju nebūtų buvę nieko, ką vieninė Quine’o aibė galėtų įtraukti. Taigi, jei Quine’as būtų neegzistavęs, vieninė Quine’o aibė, jei ji būtų egzistavusi, būtų buvusi tuščia. Bet akivaizdu, kad aibė, kurios vienintelis narys yra Quine’as, negalėtų egzistuoti būdama tuščia. Pasauliuose, kuriuose Quine’as neegzistuoja, neegzistuoja ir jo vieninė aibė. Ir, žinoma, tas pats galioja aibėms, kurios įtraukia Quine’ą kartu su kitais objektais. Pavyzdžiui, filosofų aibė S – aibė, kurios nariai yra visi filosofai, – nebūtų egzistavusi, jei Quine’as nebūtų egzistavęs. Žinoma, jei Quine’as būtų neegzistavęs, būtų egzistavusi aibė, įtraukianti visus filosofus ir nieko daugiau. Bet S – aibė, kuri faktiškai įtraukia tik filosofus, – nebūtų egzistavusi.
Čia aptinkame kertinį skirtumą tarp aibių ir savybių. Nėra netapačių aibių, kurios turi tuos pačius narius, ir nėra aibės, kuri galėtų neturėti kažkurio nario, kurį ji turi, ar turėti, kurio neturi. Bet pora netapačių savybių – pavyzdžiui, būti gyvūnu su širdimi ir būti gyvūnu su kepenimis ar būti Platono mokytoju ir būti žemiausiu graikų filosofu – gali turėti tą pačią ekstensiją, o tokią savybę kaip būti riestanosiu galėjo instancijuoti kažkas, kas faktiškai jos neinstancijuoja. Galime įvardyti šį skirtumą taip – visos aibės, bet ne visos savybės turi savo ekstensiją esmingai. Tačiau, jei taip, tai aktualistams šiuo atžvilgiu privalu nesekti kanoninės schemos ir neteigti, kad savybės yra funkcijos iš galimų pasaulių į aibes individų. Jei jokia Quine’ą įtraukianti aibė neegzistuoja nė viename pasaulyje, kuriame neegzistuoja Quine’as, tai tas pat turi būti sakoma ir apie bet kokią aibę, kurios tranzityvus uždarymas įtraukia Quine’ą. Taigi, savybės negali būti funkcijos iš pasaulių į aibes individų, mat jei taip būtų, tai tada, jei Quine’as būtų neegzistavęs, būtų neegzistavusios ir jokios jo savybės – o tai yra absurdiška.
Tad, kaip aktualistai mes turime atmesti kanoninę savybių sampratą. Savybės nėra funkcijos ar kažkokia aibė, kurios tranzityvus uždarymas įtraukia atsitiktinius objektus. Tačiau turime pritarti kanoninei sampratai ir tarti, kad savybės yra tokio pobūdžio dalykai, kurie yra instancijuojami objektų ir instancijuojami objektų galimuose pasauliuose. Objektas x turi savybę P pasaulyje W, jei W įtraukia x-o buvimą P. Pavyzdžiui, Quine’as turi savybę būti įžymiu filosofu. Kadangi šitai galioja, tai jis turi šią savybę faktiniame pasaulyje α. Be jokios abejonės, jis taip pat turi šią savybę ir daugelyje kitų pasaulių. Abstraktūs objektai, kaip ir konkretūs objektai, turi savybes pasauliuose. Skaičius 9 turi savybę būti planetų skaičiumi pasaulyje α, bet kai kuriuose kituose pasauliuose 9-ui trūksta šios savybės ir vietoj to 9-as turi šios savybės neigimą. Teiginys
(7) Quine’as yra įžymus filosofas
turi savybę teisinga faktiniame pasaulyje. Kai kuriuose kituose pasauliuose šis teiginys yra klaidingas. Savybė P yra esminė objektui x, jei x turi P visuose pasauliuose, kuriuose x egzistuoja. Kita vertus, x turi P atsitiktinai, jei x turi P, bet neturi jos esmingai. Taigi, Quine’as turi savybę būti filosofu atsitiktinai. Bet, be jokios abejonės, savybė būti asmeniu yra jam esminė. Teiginys (7) turi teisingumą atsitiktinai, bet
(8) Visi įžymūs filosofai yra filosofai
turi teisingumą esmingai. Išties, būtinas teiginys ir yra teiginys, kuris turi teisingumą esmingai. Taigi, mes galime suprasti de dicto modalumus kaip ypatingą de re modalumų atvejį. Kai kurios savybės – pavyzdžiui, teisingumas – yra esminės kai kuriems dalykams, kurie ją turi, ir atsitiktinės kitiems. Kitos, pavyzdžiui, kaip tapatybė sau, yra esminė visiems objektams ir išties būtinai esminė visiems objektams, t. y. teiginys
(9) Viskas esmingai tapatu sau
yra būtinai teisingas. Dar kitos savybės yra esminės tiems objektams, kurie jas turi, bet jas turi tik dalis objektų, pavyzdžiui, būti skaičiumi ar būti asmeniu.
Tarp visiems objektams esminių savybių patenka ir egzistavimas. Kai kurie filosofai įrodinėjo, kad egzistavimas nėra savybė. Tačiau jų samprotavimai, net ir tada, kai jie nuoseklūs, rodos, daugių daugiausia parodo tik tiek, kad egzistavimas yra ypatingos rūšies savybė. Ir išties ji yra ypatinga: kaip ir tapatybė sau, egzistavimas yra esminė kiekvienam objektui, dargi būtinai esminė. Mat gana akivaizdu, kad kiekvienas objektas turi egzistavimą kiekviename pasaulyje, kuriame jis egzistuoja. Tačiau tai nereiškia, kad kiekvienas objektas yra būtina esatis. Būtina esatis yra tokia esatis, kuri egzistuoja kiekviename galimame pasaulyje. Tuo pasižymi tik kai kurie objektai: skaičiai, savybės, grynosios aibės, teiginiai, dalykų padėtys, Dievas. Daugelis filosofų manė, kad negalėtų būti būtinų esačių, kad jokiame galimame pasaulyje nėra esaties, kuri egzistuoja visuose galimuose pasauliuose. Bet, žvelgiant iš dabartinio požiūrio taško, tai milžiniška klaida. Akivaizdu, kad yra bent tiek pat būtinų esačių, kiek ir atsitiktinių.
Tarp būtinų esačių yra ir dalykų padėtys, taigi, ir patys galimi pasauliai. Objektas x egzistuoja pasaulyje W, jei ir tik jei nėra galima, kad W būtų faktinis ir x neegzistuotų. Iš to seka, kad kiekvienas galimas pasaulis egzistuoja kiekviename galimame pasaulyje, tad ir savyje. Pavyzdžiui, pasaulis α egzistuoja pasaulyje α. Ši mintis sulaukė kažkiek pasipriešinimo, bet, kiek man teko matyti, ne kokiu nors įtikinamu pagrindu. Galimas pasaulis W yra dalykų padėtis. Kadangi nėra galima, kad W neegzistuotų, tai nėra galima, kad W būtų faktinis ir W neegzistuotų. Bet būtent tai ir reiškia pasakymas, kad W egzistuoja pasaulyje W. Taigi, kiek matau, tai, kad α egzistuoja pasaulyje α, yra visai neproblemiška.
3. Esmė ir α-transformacija. Tarp objektui esminių savybių yra viena (ar kelios) ypač svarbi: tai objekto esmė, individuali prigimtis ar, vartojant Škoto terminą, šitybė. Aš vartosiu žodį „esmė“, mat jis lengvesnis. Ne Škotas atrado esmes. Jas aptarė jau Boecijus, kuris reikalą išdėstė taip:
Mat jei būtų galima išgalvoti vardą, tai tą vieninę ir jokiai kitai subsistencijai neperteikiamą kokybę praminčiau išgalvotu jos vardu, kad to, kas teigta, forma taptų aiškesnė. Tebūna ta neperteikiama Platono savybė pavadinama platoniškumu. Juk tą kokybę – platoniškumą – galime praminti išgalvotu žodžiu taip, kaip žmogaus kokybę vadiname žmogiškumu. Vadinasi, šis platoniškumas priklauso tik vienam žmogui ir ne bet kokiam, o vieninteliam Platonui.
Kiek man žinoma, tai ankstyviausias eksplicitiškas individualių esmių aptarimas. Šiuo pagrindu „boecionizmu“ galime įvardyti pažiūrą, kad esama esmių. Remiantis Boecijaus samprata, Platono esmė yra savybė, kurią jis turi esmingai; dargi ji yra „jokiai kitai subsistencijai neperteikiama“ ta prasme, kad nėra galimo pasaulio, kuriame egzistuoja kažkas, kas jam netapatu ir ją turi. Galime sakyti, kad ji yra jam esminė ir esmingai jam unikali. Viena tokia savybė, teigia Boecijus, yra savybė būti Platonu ar savybė būti tapačiam Platonui. Kai kurie žmonės reiškia pasipriešinimą tokių savybių pripažinimui, bet visai neaišku, kokiu pagrindu. Bet kuriuo atveju labai paprasta nusakyti sąlygas, kurias išpildęs objektas turi platoniškumą: ganėtinai akivaizdu, kad objektas jį turi, jei ir tik jei tas objektas yra Platonas.
Bet tai nėra vienintelė Platono esmė. Norėdami sužinoti, kokios yra kitos, turime pastebėti, kad Platonas turi pasauliu indeksuotas savybes. Bet kokios savybės P ir pasaulio W atžvilgiu egzistuoja pasauliu indeksuota savybė P pasaulyje W. Objektas x instancijuoja P pasaulyje W, jei W įtraukia x buvimą P. Mes jau susidūrėme su viena pasauliu indeksuota savybe: teisingumu pasaulyje α. Teisingumas pasaulyje α apibūdina visus teiginius, kurie yra faktiškai teisingi. Dargi tai juos apibūdina kiekviename galimame pasaulyje. Esama pasaulių, kuriuose teiginys
(7) Quine’as yra įžymus filosofas
neturi teisingumo, bet nėra tokių, kuriuose jis neturi teisingumo pasaulyje α. (7) galėjo būti klaidingas, bet net jei jis būtų buvęs klaidingas, α vis tiek būtų įtraukęs (7) teisingumą, tad (7) būtų buvęs teisingas pasaulyje α. Teisingumas pasaulyje α yra neatsitiktinė savybė: kiekvienas objektas esmingai turi ją arba jos neigimą. Ir lygiai tas pats pasakytina apie kiekvieną pasauliu indeksuotą savybę: jei P yra pasauliu indeksuota savybė, tai nėra objekto, kuris turi P arba jos neigimą atsitiktinai.
Kur P yra savybė, tai sakykime, kad pasauliu indeksuota savybė P pasaulyje α (pavadinkime ją „Pα“) yra P α-transformacija. Jei 𝒫 yra predikatas, išreiškiantis savybę P, tai jo α-transformacija 𝒫α išreiškia Pα. Dabar pagalvokime apie bet kokią savybę Q, kurią turi tik Quine’as: pavyzdžiui, būti „Žodžio ir objekto“ autoriumi ar būti gimus P, T, kur P yra vieta, kurioje gimė Quine’as, o T – tai laikas, kada gimė Quine’as. Q yra atsitiktinė Quine’o savybė, bet jos α-transformacija Qα jam esminė. Išties, Qα yra viena iš Quine’o esmių. Prisiminkime, tam, kad savybė E būtų Quine’o esme, ji turi būti jam esminė ir tokia, kad nėra galimo pasaulio, kuriame egzistuoja jam netapatus objektas, turintis E. Kadangi Qα yra indeksuota pasauliu, tai ji išpildo pirmą sąlygą. Tačiau ji taip pat išpildo ir antrąją. Kad šituo įsitikintume, turime pirma pastebėti, kad savybė būti tapačiam Quine’ui yra esminė bet kam, kas ją turi, t. y.
(10) būtina, kad bet kas, tapatus Quine’ui, turi būti tapatus Quine’ui esmingai.
Tačiau tada iš to seka, kad bet kas, kas turi būti tapatus Quine’ui neigimą, t. y. skirtingumą nuo Quine’o, turi šią savybę esmingai:
(11) būtina, kad bet kas, skirtingas nuo Quine’o, turi skirtingumą nuo Quine’o esmingai.
Taip pat turime pastebėti, kad
(12) būtina, kad objekto x esmė griežtai implikuoja kiekvieną savybę, kuri yra esminė x,
kur savybė P griežtai implikuoja savybę Q, jei nėra galima, kad P būtų instancijuota objekto, kuris neturi Q. Ir dabar tarkime, kad yra pasaulis W, kuriame egzistuoja Quine’ui netapatus objektas x, kuris turi Qα. Tada privalo būti esmė E, kuri yra instancijuota pasaulyje W ir kuri griežtai implikuoja (11) ir (12): tiek būti netapačiam Quine’ui, tiek Qα. Kadangi E griežtai implikuoja Qα, tai E yra instancijuota pasaulyje α – ir instancijuota kažkokio objekto, kuris yra netapatus Quine’ui ir turi Q. Bet, remiantis pradine prielaida, pasaulyje α nėra nieko, kas būtų netapatus Quine’ui ir turėtų Q. Taigi, Qα yra Quine’o esmė.
Vadinasi, bet kurios Quine’ui unikalios savybės P α-transformacija Pα yra viena iš jo esmių. Taigi, bet kuriai Quine’ą nurodančiai apibrėžiamajai deskripcijai (ιx)Fx esama deskripcijos (ιx)Fαx, kuri Quine’ą nurodo esmingai – jį išskiria išreikšdama vieną iš jo esmių. Čia, mūsų nuomone, glūdi Keitho Donnellano (1974) aptarto reiškinio paaiškinimas. Jis tvirtina, kad sakinys su deskripcija kartais gali būti vartojamas išreikšti teiginį, ekvivalentų tam, kuris išreiškiamas sakiniu, gaunamu tą deskripciją pakeitus į ja nurodomo objekto tikrinį vardą. Tad sakinys
(13) Žodžio ir objekto autorius yra sumanus
gali būti vartojamas išreikšti teiginį, ekvivalentų
(14) Quine’as yra sumanus.
Sakiniu (13) išreikštas teiginys yra teisingas pasaulyje W, kuriame ne Quine’as, bet kažkas kitas, tarkime, Geraldas R. Fordas, parašo Žodį ir objektą, jei ir tik jei Quine’as yra sumanus pasaulyje W – nėra svarbu, pasaulyje W Fordas sumanus ar ne. Šį reiškinį galime suprasti kaip implicitinį α-transformacijos pritaikymą deskripcijai „Žodžio ir objekto autorius“. Tad tai, ką išreiškia (13), gali būti ekplicitiškiau nusakyta teiginiu
(15) (Žodžio ir objekto autorius)α yra sumanus,
teiginiu, teisingu tuose pačiuose pasauliuose, kuriuose teisingas ir (14).
Donnellanas pastebėjo, kad šis reiškinys aptinkamas sakiniuose su deskripcijomis. Tačiau bet kuriam predikatui 𝒫 esama jo α-transformacijos 𝒫α. Taigi, turėtume tikėtis, jog Donnellano reiškinys pasirodys ir kituose kontekstuose – pavyzdžiui, universaliuosiuose sakiniuose. Šie spėjimai pasitvirtina. Kreipdamasis į Alpių klubo narius, aš sakau
(16) kiekvienas Alpių klubo narys yra puikus alpinistas!
Iš principo, jei daugžodžiavimas taip neįgristų, galėjau perbėgti per narių sąrašą, tardamas tokį ilgą konjunkcinį sakinį:
(17) N1 yra puikus alpinistas & N2 yra puikus alpinistas & … & Nn yra puikus alpinistas,
kur kiekvienam klubo nariui esama konjunkto, prijungiančio „yra puikus alpinistas“ prie jo vardo. Jei M1…Mn yra klubo nariai, tai teiginys, išreikštas sakiniu (16), yra teisingas duotajame pasaulyje W, tik jei kiekvienas M1…Mn yra puikus alpinistas pasaulyje W. Nėra svarbus faktas, jei tai faktas, kad pasaulyje W klube yra ne alpinistų ar ne puikių alpinistų. Bet tada (16) galima eksplicitiškiau nusakyti kaip
(18) kiekvienas (Alpių klubo narys)α yra puikus alpinistas.
Galime šį reikalą aptarti ir kiek kitaip. Tarkime, kad „S“ – tai aibės, kurios nariai yra Alpių klubo nariai, vardas. Tada (16), (17) ir (18) išreiškia teiginį, ekvivalentų
(19) kiekvienas S narys yra puikus alpinistas.
Žinoma, jei vartojame (16) eksplicitiškai nepritaikę α-transformacijos, tada tai, ką tvirtiname, nėra ekvivalentu (19): mat tokiu atveju tai, ką mes tvirtiname, yra teisinga pasaulyje W, tik jei pasaulyje W visi Alpių klubo nariai yra puikūs alpinistai.
4. Sritys ir teiginiai. Bet grįžkime prie mums svarbiausio dalyko. Kaip aktualistai mes atmetame kanoninę savybių sampratą ir, nepaisant to, priimame tai, kad objektai turi savybes pasauliuose, ir tai, kad kai kurios jų savybės jiems yra esminės. Tarp objektams esminių savybių mes pabrėžėme jų esmes. O kaip yra su sritimis? Remiantis kanonine samprata, kiekvienas galimas pasaulis turi sritį: aibę objektų, kurie jame egzistuoja. Čia turiu dvi pastabas. Pirma, kam skirtos sritys? Savaime suprantama, kad kvantoriai per jas kvantifikuotų. Bet čia reikia būti atsargiems. Remiantis įprasta sričių ir kintamųjų samprata, kvantifikacija suprantama tokiu būdu. Aptarkime tokį universaliai kvantifikuotą sakinį:
(20) Visi dėmėti šunys yra draugiški
arba
(20) (x) (jei x yra taškuotas šuo, tai x yra draugiškas).
Sakome, kad kvantorius kvantifikuoja per aibę objektų D: tai, ką sako (20), yra teisinga, jei ir tik jei kiekvienas srityje D esantis taškuotas šuo taip pat yra draugiškas. Viskas čia, regis, neblogai – kodėl turėtume būti atsargūs? Nes tai gali įteigti mintį, kad (20) išreiškia teiginį, ekvivalentų, jei ne tapatų, teiginiui
(21) kiekvienas D narys yra draugiškas, jei jis yra taškuotas šuo,
kur D – tai sakinyje (20) esančio kvantoriaus sritis. O ši mintis akivaizdžiai klaidinga. Pagalvokime apie galimą pasaulį, kuriame egzistuoja aibė D ir jos nariai – pastarieji yra, jei dėmėti šunys, tai draugiški, – ir kur taip pat yra kitų dėmėtų šunų – srityje D nesančių šunų, kurie yra pikti ir irzlūs. Tai, ką išreiškia (21), tame pasaulyje yra teisinga. Tačiau tai, ką išreiškia (20), ten yra aiškiai klaidinga. (20) ir (21) yra materialiai, bet ne logiškai ekvivalentūs: jie abu teisingi arba abu klaidingi, bet jie nėra teisingi tuose pačiuose pasauliuose. Jei norime, galime sakyti, kad formą „(x)Fx“ turinčiame sakinyje kvantorius turi sritį D. Bet tokiu sakiniu išreikštas teiginys įprastai nebus ekvivalentus tvirtinimui, kad kiekvienas D narys turi F.
Pereikime prie antros ir šiame kontekste svarbesnės pastabos. Remiantis kanonine schema, kiekvienas pasaulis W turi sritį – aibę objektų, kurie egzistuoja pasaulyje W. Nors tai išsakoma retai, visada kaip savaime suprantamas faktas priimama tai, kad galimas pasaulis W su sritimi ψ(W) esmingai pasižymi savybe turėti ψ(W) kaip savo sritį. Turėti ψ(α) kaip sritį yra esminga pasauliui α – jei kitas pasaulis β būtų buvęs faktinis, galbūt kiti individai būtų egzistavę, bet ψ(α) vis tiek būtų buvusi α sritis. Tačiau, remiantis aktualistinėmis nuostatomis, ši pora tvirtinimų, t. y.
(22) bet kuriam pasauliui W esama aibės ψ(W), kuri įtraukia tik pasaulyje W
egzistuojančius objektus,
ir
(23) jei D yra pasaulio W sritis, tai W esmingai turi savybę turėti D kaip savo sritį,
sukelia sunkumų. Mat, kaip jau aptarėme anksčiau, aibė gali egzistuoti tik tuose pasauliuose, kuriuose egzistuoja visi jos nariai. Taigi, ψ(α) nebūtų egzistavusi, jei bet kuris jos narys nebūtų egzistavęs. Vadinasi, ψ(α) nebūtų egzistavusi, jei, tarkime, Sokratas nebūtų egzistavęs. Bet jei, kaip tvirtina (23), pasaulis α esmingai turi savybę būti toks, kurio sritis yra ψ(α), tai α gali egzistuoti, tik jei egzistuoja ψ(α). Tad, jei Sokratas būtų neegzistavęs, tai tas pat būtų galioję ir sričiai ψ(α), ir pačiam pasauliui α. Jei priimame (22) ir (23), tai turime priimti bauginamą išvadą, kad galimi pasauliai nėra būtinos esatys: net ir visai nereikšmingas paplūdimyje gulintis akmenukas pasižymi savybe būti toks, kuris jei būtų neegzistavęs, tai išvis nebūtų buvę pasaulio α (ir bet kurio kito pasaulio, kurio sritis įtraukia tą akmenuką).
Šis sunkumas sukelia kitą sunkumą kanonin>ei teiginių sampratai, pagal kurią teiginiai yra esatys iš aibių teorijos – tarkime, aibės galimų pasaulių. Ši samprata bet kuriuo atveju turi būti atmesta, mat ji griežtai implikuoja, kad nėra netapačių, bet logiškai ekvivalenčių teiginių. Tačiau akivaizdu, kad tai yra klaidinga.
(24) Visi viengungiai yra nevedę
ir
(25) 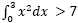
yra ekvivalentūs. Tačiau yra žmonių, kurie įsitikinę pirmuoju teiginiu, bet kurie nėra įsitikinę ar net nesupranta antrojo. Taigi, pirmasis turi savybę, kurios neturi antrasis, tad jie netapatūs. Bet pamatinis sunkumas kanoninei sampratai kyla iš apgailėtino aibių ir sričių trapumo – iš jų apgailėtino polinkio neegzistuoti pasauliuose, kuriuose neegzistuoja kai kurie jų nariai. Mat paimkime bet kokį teisingą teiginį p. Remiantis kanonine samprata, p yra aibė pasaulių, kuri įtraukia α. Bet dabar tarkime, kad kažkoks objektas – pavyzdžiui, Tadž Mahalis, – būtų neegzistavęs: tada nebūtų egzistavusi nei sritis ψ(α), nei pasaulis α, nei teiginys p. Taigi, jei Tadž Mahalis nebūtų egzistavęs, tai tas pat galiotų ir tokioms tiesoms kaip 7 + 5 = 12 ir Sokratas buvo išmintingas. Šitai yra absurdas. Remiantis kanonine samprata, pasirodo, kad tik būtinai klaidingi teiginiai kartu su tokiais, kaip
(26) nėra atsitiktinių esačių,
yra būtinos esatys. Tokio išskirtinio statuso jie tikrai nenusipelno.
Kaip tada mums, aktualistams, reikėtų suprasti galimų pasaulių sritis? Jei norime, galime sutikti su kanonine samprata ir teigti, kad kiekvienam pasauliui W išties esama aibės ψ(W), kuri įtraukia tik pasaulyje W egzistuojančius objektus. Tačiau, remiantis aktualistinėmis pažiūromis, sritys nėra jau tokios svarbios. Jos taip pat pasižymi tam tikromis anomaliomis savybėmis. Pirma, kaip ką tik matėme, sritys įprastai yra atsitiktinės esatys. Jei Sokratas būtų neegzistavęs, jokia jį įtraukianti aibė nebūtų egzistavusi, taigi nebūtų egzistavusi ir sritis ψ(α). Betgi galimi pasauliai yra būtinos esatys. Taigi, pasauliai įprastai neturi savo srities esmingai. Jei Sokratas būtų neegzistavęs, tai būtų buvusi aibė, netapati aibei ψ(α), kuri būtų buvusi pasaulio α sritis, o jei nebūtų egzistavusi nė viena atsitiktinė esatis, tai pasaulio α sritis būtų įtraukusi tik būtinas esatis. Antra, bet kurio galimo pasaulio W sritis, žvelgiant iš aktualistinės perspektyvos, yra aibės ψ(α) poaibis. Kadangi nėra objektų, kurie netapatūs egzistuojantiems pasaulyje α, tai ψ(W) negali įtraukti jokio objekto, kuris nėra tapatus nė vienam egzistuojančiam pasaulyje α. Aktualistas, žinoma, noriai sutiks, kad galėjo būti objektas, netapatus nė vienam egzistuojančiam pasaulyje α. Taigi, yra galimas pasaulis W, kuriame egzistuoja objektas, netapatus nė vienam iš faktiškai egzistuojančių. Taigi, aktualistas privalo laikytis nuostatos, kad ψ(W) yra ψ(α) poaibis, nepaisant fakto, kad W įtraukia pasaulyje α neegzistuojančio objekto egzistavimą. Kaip įmanoma šitai suderinti? Kaip aktualistas gali suprasti
(27) galėtų egzistuoti objektas, netapatus nė vienam iš faktiškai egzistuojančių objektų,
jei jis laikosi nuostatos, kad bet kurio W atžvilgiu ψ(W) yra ψ(α) poaibis?
5. Esmės ir teisingumo sąlygos. Visai nesunkiai: jam reikia griebtis esmių. Sokratas yra atsitiktinė esatis, tačiau jo esmė – ne. Savybės, kaip ir teiginiai bei galimi pasauliai, yra būtinos esatys. Jei Sokratas būtų neegzistavęs, jo esmė būtų buvusi neinstancijuota, tačiau ne neegzistuojanti. Pasauliuose, kuriuose Sokratas egzistuoja, sokratiškumas yra jo esmė: instancijuoti sokratiškumą yra jam esminga. Tačiau sokratiškumas neturi savybės būti instancijuotam Sokrato esmingai: pasauliuose, kuriuose Sokratas neegzistuoja, jis jo neinstancijuoja. Tuose pasauliuose sokratiškumas, žinoma, išvis nėra instancijuotas: taigi, būti instancijuotam Sokrato, jei išvis instancijuotam, yra esminga sokratiškumui, o būti instancijuotam Sokrato yra jam atsitiktina.
Su kiekvienu galimu pasauliu W yra susieta aibė ψE(W) – aibė esmių, kurios yra instancijuotos pasaulyje W. ψE(W) yra W esmių sritis, o aibė esmių UE yra visų pasaulių W esmių sričių ψE(W) sąjunga. Esmių sritys turi privalumus ten, kur sritys turi trūkumus. Savybės egzistuoja kiekviename pasaulyje, vadinasi, tas pats galioja ir jų aibėms. Taigi, esmių sritys yra būtinos esatys. Dar daugiau – jei ψE(W) yra pasaulio W esmių sritis, tai W esmingai turi savybę turėti ψE(W) kaip savo esmių sritį. Lygiai kaip ir įvairios savybės kartais yra neinstancijuotos, taip pat ir esmės gali būti neinstancijuotos. Jei Sokratas būtų neegzistavęs, tada sokratiškumas būtų buvęs neinstancijuota esmė. Labai tikėtina, kad faktiškai yra neinstancijuotų esmių: tikriausiai yra pasaulis, kurio esmių sritis ψE(W) įtraukia faktiškai neinstancijuotą esmę. Taigi, be abejonės, UE įtraukia neinstancijuotų esmių.
Dabar jau esame pasirengę susitvarkyti su (27). Bet prieš tai pažiūrėkime, kaip iš aktualisto perspektyvos reikėtų suprasti paprastesnius teiginius. Aptarkime pirma
(1) (∃x) x yra violetinė karvė.
Sakinys (1) yra teisingas, jei ir tik jei kažkuris UE narys yra koinstancijuotas su savybe būti violetine karve, o (1) yra teisingas pasaulyje W, jei ψE(W) įtraukia esmę, kuri pasaulyje W yra koinstancijuota su šia savybe.
(2) Galimai (∃x) x yra violetinė karvė
yra teisingas, jei egzistuoja pasaulis, kuriame teisingas (1), t. y. jei yra esmė, kuri kažkuriame pasaulyje yra koinstancijuota su būti violetine karve. Taigi, sakinys (2) yra neatsitiktinas: arba būtinai teisingas, arba būtinai klaidingas. Kita vertus, sakinys
(3) (∃x) galimai x yra violetinė karvė
yra teisingas, jei kažkuris UE narys yra koinstancijuotas su savybe galimai būti violetine karve. Taigi, (3) yra teisingas, jei kažkuri instancijuota esmė yra kažkuriame pasaulyje koinstancijuota su savybe būti violetine karve. Kalbant bendriau, (3) yra teisingas galimame pasaulyje W, jei kažkuris ψE(W) narys kažkuriame pasaulyje W* yra koinstancijuotas su būti violetine karve. (3) griežtai implikuoja (2). Bet jei, o tai atrodo visai tikėtina, galima, kad būtų violetinė karvė, bet taip pat galima, kad nebūtų nieko, kas galėtų būti violetine karve, tai nėra taip, jog (2) griežtai implikuotų (3).
Kalbant apie vieninius teiginius, akivaizdu, jog toks teiginys, kaip
(28) Fordas yra sumanus,
yra teisingas pasaulyje W, jei ir tik jei Fordo esmė pasaulyje W yra koinstancijuota su sumanumu.
O kaip yra su
(29) Fordas nėra sumanus?
Sakinys (29) iš tikrųjų yra dviprasmis – išreiškia du visai skirtingus teiginius. Viena vertus, jis išreiškia teiginį, Fordui predikuojantį sumanumo trūkumą, – teiginį, teisingą tuose pasauliuose, kuriuose Fordo esmė yra koinstancijuota su sumanumo trūkumu. Šį teiginį eksplicitiškiau galima išreikšti taip
(29*) Fordas yra nesumanus,
t. y. Fordas turi sumanumo neigimą. Tačiau (29) taip pat išreiškia ir (28) neigimą:
(29**) nėra taip, kad Fordas yra sumanus.
Akivaizdu, kad (28) yra klaidingas pasauliuose, kuriuose Fordas neegzistuoja, taigi, (29**) tuose pasauliuose yra teisingas. Išties, kertinis skirtumas tarp (29*) ir (29**) yra tas, kad pirmasis, bet ne antrasis griežtai implikuoja, jog Fordas egzistuoja. (29**), kitaip nei (29*), yra teisingas pasauliuose, kuriuose Fordas neegzistuoja.
Skirtį tarp (29*) ir (29**) galime suprasti kaip skirtumą tarp de re ir de dicto. (29*) Fordui predikuoja savybę – nesumanumą. Kita vertus, (29**) predikuoja klaidingumą teiginiui (28), bet nepredikuoja nieko Fordui. (29*) yra teisingas tuose pasauliuose, kuriuose Fordo esmė yra koinstancijuota su nesumanumu. Kadangi nėra ir negalėtų būti neegzistuojančių objektų, nėra ir negalėtų būti neegzistuojančių nesumanumo instanciacijų. Taigi, (29*) griežtai implikuoja, kad Fordas egzistuoja. Tačiau nėra taip, kad tai griežtai implikuotų teiginys (29**): jis teisingas, kai (28) klaidingas, ir teisingas net ir tuose pasauliuose, kuriuose Fordas neegzistuoja ir neturi savybių.
Galima matyti, kad sakinio (29) dviprasmiškumas kyla dėl dviprasmybės aprėptyje. (29**) neigimo ženklas taikomas sakiniui ir įtraukia vardą „Fordas“ į savo aprėptį. Tačiau (29*) neigimo ženklas taikomas ne sakiniui, o predikatui: taip sukuriamas kitas predikatas. Šiuo atveju „Fordas“ nepatenka į neigimo aprėptį. Kai „Fordas“ turi plačiausią aprėptį, kaip (29*) atveju, tada gaunamas sakinys išreiškia teiginį, kuris predikuoja Fordui savybę ir griežtai implikuoja jo egzistavimą. Kai vardas turi siauresnę nei plačiausią aprėptį, tai gali būti, jog išreikštas teiginys nepredikuoja Fordui savybės ir jis gali būti teisingas pasauliuose, kuriuose Fordas neegzistuoja. Ši sąveika tarp de re / de dicto skirties ir dviprasmybės aprėptyje aptinkama ir kitur. Toks sakinys, kaip
(30) jei Sokratas yra išmintingas, tai kažkas yra išmintingas,
yra dviprasmis lygiai taip pat, kaip ir (29). Jį galime perskaityti kaip savybės predikaciją Sokratui: savybės būti tokiam, kuris jei jis yra išmintingas, tai kažkas yra išmintingas. Jei jį skaitome tokiu būdu, tai eksplicitiškiau galime nusakyti tai, ką jis išreiškia, taip:
(30*) Sokratas yra toks, kad jei jis yra išmintingas, tai kažkas yra išmintingas.
Šis teiginys yra teisingas tik tuose pasauliuose, kuriuose Sokratas egzistuoja. Tačiau (30) taip pat gali išreikšti teiginį, kuris predikuoja ryšį tarp teiginių Sokratas yra išmintingas ir kažkas yra išmintingas. Kadangi šie teiginiai į šį ryšį patenka kiekviename galimame pasaulyje, tai šis teiginys yra būtinai teisingas. Taigi, kitaip nei (30*), jis yra teisingas pasauliuose, kuriuose Sokratas neegzistuoja. Panašiai ir su sakiniu
(31) jei kažkas yra tapatus Sokratui, tai kažkas yra asmuo.
Jei sakinyje (31) „Sokratui“ suteikiame plačiausią aprėptį, tai juo išreiškiame Sokratui savybę predikuojantį atsitiktinį teiginį, kuris yra teisingas tik tuose pasauliuose, kuriuose egzistuoja Sokratas. Tačiau, jei jam suteikiame siauresnę aprėptį, tai (31) išreiškia būtiną teiginį, žinoma, su sąlyga, kad būti asmeniu yra esminga Sokratui.
O kaip su vieniniais egzistavimo teiginiais? Teiginys
(32) Fordas egzistuoja
yra teisingas tik tuose pasauliuose, kuriuose Fordo esmė yra koinstancijuota su egzistavimu, – pasauliuose, kuriuose Fordas egzistuoja. Tačiau
(33) Fordas neegzistuoja
yra dviprasmis lygiai taip pat, kaip ir (29): jis gali išreikšti
(33*) Fordas turi neegzistavimą (egzistavimo neigimą)
arba
(33**) nėra taip, kad Fordas egzistuoja.
(33**) yra (32) neigimas, ir jis teisingas tik tuose pasauliuose, kuriuose (32) yra klaidingas. Tačiau (33*) yra teisingas tik tuose pasauliuose, kuriuose Fordo esmė yra koinstancijuota su neegzistavimu. Kaip aktualistai mes laikomės pozicijos, kad nėra ir negalėtų būti neegzistuojančių objektų. Taigi, nėra pasaulių, kuriuose kažkuri esmė yra koinstancijuota su neegzistavimu, – (33*) yra būtinai klaidingas.
Dabar galime grįžti prie sakinio
(27) galėtų egzistuoti objektas, netapatus nė vienam iš faktiškai egzistuojančių objektų.
Remiantis kanonine samprata, (27) yra teisingas, tik jei yra toks U narys x, kuris faktiškai neegzistuoja, bet kuris egzistuoja kažkuriame pasauliui α netapačiame galimame pasaulyje. Taigi, remiantis šia samprata, (27) yra teisingas, jei ir tik jei yra objektų, kurie neegzistuoja, bet galėtų egzistuoti. Tačiau, remiantis aktualistine samprata, nėra objektų, kurie neegzistuoja. Bet kaip tada mums derėtų suprasti (27)? Visai nesunku: (27) yra teisingas, jei ir tik jei yra galimas pasaulis, kuriame
(34) yra objektas, kuris neegzistuoja pasaulyje α,
yra teisingas. Tačiau (34) yra teisingas pasaulyje W, jei ir tik jei yra esmė, kuri instancijuota pasaulyje W, bet kuri neinstancijuota pasaulyje α. Taigi, (27) yra teisingas, jei ir tik jei yra bent viena esmė, kuri yra instancijuota kai kuriuose pasauliuose, bet kuri faktiškai nėra instancijuota, – t. y. jei ir tik jei yra neinstancijuota esmė. Tad labai tikėtina, kad (27) yra teisingas. Taigi, kaip aktualistai šį reikalą galime nusakyti taip:
(35) nors galėtų būti objektų, kurie faktiškai neegzistuoja, nėra neegzistuojančių objektų,
kurie galėtų egzistuoti.
Taigi, tokios yra esminės aktualistinės galimų pasaulių sampratos dedamosios. Ji turi kanoninės sampratos privalumus, bet ne jos trūkumus: tokiu būdu galime gauti visas įžvalgas, kurias suteikia galimų pasaulių idėja, nepriimdami to, kad yra ar galėtų būti neegzistuojančių objektų.
Literatūra
Adams, R., 1974. Theories of Actuality. Noûs 8: 211–231.
Castañeda, H. N., 1975. Individuation and Non-identity: a New Look. American Philosophical Quarterly 12 (2): 131–140.
Donnellan, K., 1974. Speaking of Nothing. Philosophical Review 83: 3–31.
Kripke, S., 1963. Semantical Considerations on Modal Logic. Acta Philosophica Fennica 16: 83–94. Reprinted in Reference and Modality, ed. Linksy. Oxford, 62–72.
Lewis, D., 1972. General Semantics. In: Semantics of Natural Language, eds. D. Davidson, G. Harman. Dordrecht: Springer, 169–218.
Montague, R., 1974. Formal Philosophy. Edited by R. M. Thomason. New Haven: Yale University Press.
Plantinga, A., 1974. The Nature of Necessity. Oxford: Clarendon.
Plantinga, A., 1978. The Boethian Compromise. American Philosophical Quarterly 15 (2): 129–138.
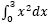 . Bet, žinoma, jos nėra viena ir ta pati savybė. Jei ontologinis įrodymas yra korektiškas, tai savybė žinoti, kad Dievas neegzistuoja, yra būtinai koekstensyvi savybei būti apskritu kvadratu. Bet, žinoma, jos nėra ta pati savybė, net jei tas įrodymas korektiškas.
. Bet, žinoma, jos nėra viena ir ta pati savybė. Jei ontologinis įrodymas yra korektiškas, tai savybė žinoti, kad Dievas neegzistuoja, yra būtinai koekstensyvi savybei būti apskritu kvadratu. Bet, žinoma, jos nėra ta pati savybė, net jei tas įrodymas korektiškas.