Problemos ISSN 1392-1126 eISSN 2424-6158
2020, vol. 97, pp. 132–149 DOI: https://doi.org/10.15388/Problemos.97.11
Temporalinės logikos sistemų CL ir Kb semantinės interpretacijos su tradicinių teisingumo reikšmių pertrūkiais
Živilė Pabijutaitė
Vilniaus universiteto
Filosofijos istorijos ir analitinės filosofijos katedra
E. paštas zivile.pabijutaite@fsf.vu.lt
ORCID https://orcid.org/0000-0002-4928-7298
Santrauka. Nuo XX a. vidurio temporalinės logikos srityje buvo sukurta bent keliolika konkuruojančių semantinių teorijų, pateikiančių skirtingus atsitiktinių teiginių apie ateitį vertinimo kriterijus. Straipsnyje nagrinėjamos dviejų temporalinės logikos sistemos Kt plėtinių – CL (Cocchiarella Linear) ir Kb (Kripke Branching) – semantinės interpretacijos, kuriose tokiems teiginiams būdingi standartinių teisingumo reikšmių pertrūkiai: 1) J. Łukasiewicziaus Ł3; 2) S. C. Kleene’o K3; 3) A. Prioro okamizmas; 4) R. Thomasono supervaluacionizmas; 5) J. MacFarlane’o reliatyvizmas. Šio straipsnio tikslas – pateikti išsamią minėtų semantinių teorijų tipologiją ir vertinimą pagal šiuos kriterijus: a) gebėjimą pagrįsti retrospektyvų teiginių vertinimą; b) teorijos adekvatumą sprendžiant paralelią visažinystės ir atviros ateities santykio problemą; c) santykį su negalimo trečiojo dėsniu; d) santykį su kitomis indeterministiniame kontekste intuityviai priimtinomis formulėmis. Straipsnyje ginama tezė, jog vienintelė teorija, visiškai tenkinanti visus keturis išsikeltus kriterijus, yra J. MacFarlane’o reliatyvizmas, tačiau ir joje susiduriama su rimtais sunkumais svarstant retrospektyvų teiginių vertinimą teologiniame kontekste.
Pagrindiniai žodžiai: atsitiktiniai teiginiai, determinizmas, temporalinė logika, dvireikšmiškumas
Semantical Interpretations of the Temporal Logic Systems CL and Kb with the Gaps of Traditional Truth-values
Abstract. Over the past several decades, in the field of temporal logic there have been created a great number of semantical theories that provide different truth conditions for tensed propositions. In this article we deal with five non-bivalent semantical interpretations of the temporal logic systems CL (Cocchiarella Linear) and Kb (Kripke Branching): 1) Ł3 by J. Łukasiewicz; 2) K3 by S. C. Kleene; 3) Ockhamism by A. Prior; 4) supervaluationism by R. Thomason; 5) relativism by J. MacFarlane. The aim of this article is to present a detailed typology of the five semantical theories based on these criteria: a) the ability to deal with the problem of retrospective evaluation of future contingent propositions; b) the ability to deal with the problem of divine omniscience and free will; c) their relation to the law of excluded middle; d) their relation to other formulas that are intuitively acceptable in an intederministic context. It is argued that the only theory that satisfies all four criteria is the relativism of J. MacFarlane; however, it faces some serious challenges when dealing with the problem of retrospective evaluation of future contingent propositions in the theological context.
Keywords: future contingents, determinism, temporal logic, bivalence
Received: 12/11/2019. Accepted: 27/01/2020
Copyright © Živilė Pabijutaitė, 2020. Published by Vilnius University Press.
This is an Open Access article distributed under the terms of the Creative Commons Attribution Licence (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
1. Atsitiktinių teiginių apie ateitį problema ir galimi jos sprendimo būdai
Atsitiktinių teiginių apie ateitį problema – tai klausimas, ar galima (jei galima, tai kokiu būdu) priskirti tradicines teisingumo reikšmes teisinga arba klaidinga būsimojo laiko teiginiams, išreiškiantiems vien tik galimai įvyksiančią – tokią, kuri nėra nei prieštaringa, nei būtina – dalykų padėtį. Aristotelio De interpretatione devintajame skyriuje pateikiamas jūrų mūšio samprotavimas1 laikomas viena ankstyviausių ir istoriškai įtakingiausių atsitiktinių teiginių apie ateitį problemos formuluočių. Čia pateikiama supaprastinta šio samprotavimo versija:
1) kiekvienas teiginys apie praeitį, dabartį ir ateitį yra teisingas arba klaidingas;
2) teiginys yra teisingas, jei ir tik jei egzistuoja jį atitinkanti dalykų padėtis;
3) teiginys yra klaidingas, jei ir tik jei egzistuoja jam priešinga dalykų padėtis;
∴ jau dabar egzistuoja apibrėžta viena būsimų įvykių eiga2.
Išspręsti atsitiktinių teiginių apie ateitį problemą – tai rasti įtikinamą būdą, kaip išvengti šio samprotavimo išvados. Nesutinkant su šio pagrįsto samprotavimo išvada, reikia atmesti bent vieną jo prielaidų: arba visuotinį dvireikšmiškumo principo galiojimą (prielaida (1)), arba korespondencinę (arba kitaip – klasikinę) tiesos teoriją (prielaidos (2) ir (3))3.
Šio straipsnio objektas – problemos sprendimų, paremtų pirmosios prielaidos atmetimu, grupė. Ši sprendimų grupė yra vienijama pažiūros, vadinamos semantiniu inkompatibilizmu (remiantis ja, atviros ateities intuicija ir visuotinis dvireikšmiškumo principo galiojimas yra tarpusavyje nesuderinamos idėjos), ir bendroje galimų problemos sprendimų tipologijoje atrodo taip, kaip pateikta 1 schemoje.
1 schema

Semantiniai inkompatibilistai, sutikdami, jog atsitiktiniai teiginiai apie ateitį išreiškia prasmingą turinį, neigia, jog tokiems teiginiams gali būti taikomas dvireikšmiškumo principas. Dvireikšmiškumo principo galiojimas gali būti apribojamas dviem būdais – arba nepriskiriant atsitiktiniams teiginiams apie ateitį jokios reikšmės ir išpažįstant teisingumo reikšmių pertrūkius (truth-value gaps), arba priskiriant tokiems teiginiams kitą, trečią teisingumo reikšmę. Šiame straipsnyje bus nagrinėjami abu šie dvireikšmiškumo principo apribojimo būdai, kurių rezultatas čia įvardijamas kaip tradicinių teisingumo reikšmių pertrūkiai plačiąja to žodžio reikšme.
Tolesniuose darbo skyriuose nagrinėjamos šios semantiniam inkompatibilizmui atstovaujančios teorijos: i) J. Łukasiewicziaus Ł3; ii) S. C. Kleene’o K3; iii) A. N. Prioro okamizmas; iv) R. Thomasono supervaluacionizmas; v) J. MacFarlane’o reliatyvizmas.
Straipsnio tikslas yra pateikti išsamią aptariamos sprendimų grupės analizę remiantis šiais kriterijais:
a) teorijos santykiu su negalimo trečiojo dėsniu, kuris čia formuluojamas būsimuoju laiku – Fp v F~p. Kadangi ši išraiška, tesakanti, jog „Rytoj jūrų mūšis įvyks arba rytoj jūrų mūšis neįvyks“, atrodo tarsi tautologija, teorijos, išlaikančios negalimo trečiojo dėsnį, bus laikomos pranašesnėmis už šio dėsnio neišlaikančias;
b) galimybe išreikšti alternatyvias ateities galimybes – t. y. galimybe išraiškai ♢Fp & ♢F~p (kai abu F operatoriai nurodo į ateities momentus, vienodai nutolusius nuo dabarties momento4), sakančiai, jog „Gali būti, jog jūrų mūšis įvyks, ir gali būti, jog jūrų mūšis neįvyks“, būti išpildomai;
c) gebėjimu pagrįsti retrospektyvų teiginių vertinimą – remiantis šiuo kriterijumi, pranašesnėmis bus laikomos tos semantinės teorijos, kuriose esama galimybės suderinti dvi prieštaraujančias intuicijas: pagal vieną jų, teiginys Fp, kol įvykis p dar nėra įvykęs, nėra nei teisingas, nei klaidingas, pagal kitą – įvykiui p jau įvykus ir vėlesniu laiko momentu atliekant retrospektyvų teiginio Fp vertinimą, jam priskiriama reikšmė teisinga arba klaidinga;
d) teorijos adekvatumu sprendžiant paralelią visažinystės ir atviros ateities santykio problemą, kurios formuluotė pateikiama penktajame darbo poskyryje.
Taigi, pagrindinis straipsnio siekinys – ši tipologija, turėsianti parodyti, kuri iš nagrinėjamų teorijų geriausiai atitinka mūsų intuityvius įsitikinimus apie laiko tėkmę bei jos sąsajas su tiesa ir galimybe (žr. 2 schemą).
2 schema
Straipsnyje naudojamas lyginamosios analizės metodas reikalauja padaryti porą svarbių pastabų. Šiuolaikinėje temporalinėje logikoje laikinį matmenį turinčias išraiškas įprasta užrašyti pasitelkiant A. N. Prioro (1914–1969) įvestus laikinius operatorius (Prior 1957, 1967)5, o šių išraiškų teisingumo sąlygas nusakyti naudojant kiek kitaip interpretuotą S. Kripke’ės galimų pasaulių semantiką (Kripke 1959, 1963). Kai kurios šiame straipsnyje nagrinėjamos teorijos buvo sukurtos dar iki pastarųjų Prioro ir Kripke’ės atradimų (pavyzdžiui, J. Lukasiewicziaus sistema Ł3, sukurta 1920 m., arba S. C. Kleene’o sistema K3, pasirodžiusi 1952 m.), tačiau, siekiant kuo aiškiau atskleisti ankstyvųjų teorijų privalumus ir trūkumus vėlesnių teorijų atžvilgiu, jose pateikiamos atsitiktinių teiginių apie ateitį semantinės charakteristikos bus persakytos pagal šiuolaikinius standartus (jie apibūdinami kitame darbo poskyryje).
Atlikus penkių semantiniam inkompatibilizmui atstovaujančių teorijų analizę ir sudarius išsamią jų tipologiją, darbe ginama tezė, jog vienintelė tradicinių teisingumo reikšmių pertrūkiais paremta teorija, visiškai tenkinanti visus keturis išsikeltus kriterijus, yra J. MacFarlane’o reliatyvizmas, tačiau ir joje susiduriama su rimtais sunkumais svarstant retrospektyvų teiginių vertinimą teologiniame kontekste.
2. Laikinį matmenį turinčių išraiškų formalizavimas ir teisingumo sąlygos temporalinėje teiginių logikoje
Šio poskyrio tikslas – trumpai nusakyti pagrindinius temporalinės teiginių logikos, paremtos laiko momentais6, sintaksės ir semantikos principus, kuriais bus vadovaujamasi šiame straipsnyje.
Būtina pastebėti, kad teiginio samprata, kuria paprastai remiamasi temporalinėje logikoje bei kuria bus vadovaujamasi šiame tekste, smarkiai skiriasi nuo kituose kontekstuose šiandien paplitusios teiginio sampratos. Įprasta manyti, kad teiginio statusą turi tokios išraiškos, kurių teisingumas nepriklauso nuo jų išsakymo aplinkybių (pavyzdžiui, Karvės kailis yra trumpesnis nei avies arba Pirmoji 1992-ųjų metų diena yra trečiadienis), o tokios išraiškos kaip Aš priklausau daugiau nei vienai bendruomenei arba Ten vyksta kažkas įdomaus laikomos nepilnomis tol, kol jose nėra specifikuotas aš, ten bei kitų į juos panašių indeksinių žodžių konkretus turinys (taigi, išraiškos Ten vyksta kažkas įdomaus ir Čia vyksta kažkas įdomaus čia gali būti laikomos skirtingais sakiniais (sentence, statement), išreiškiančiais tą patį teiginį (proposition)). Nors nepilnais analogiškai būtų galima laikyti ir tokius teiginius kaip Rytoj įvyks jūrų mūšis – tol, kol ši išraiška nėra perrašoma panaikinant joje bet kokį temporalinį indeksiškumą, – klasikine A. Prioro tradicija besiremiančioje temporalinėje logikoje vadovaujamasi kiek kitokia, dar Antikoje ir viduramžiais susiformavusia laikinį matmenį turinčių teiginių samprata. Ankstyvosiose Antikos ir viduramžių laiko logikos plėtotėse beveik be išimčių operuojama teiginiais, kuriuose, nors ir pasižyminčiuose laikiniu turiniu, arba išvis nepateikiamos konkrečios laiko nuorodos, arba jos yra indeksinės (priklausančios nuo teiginio išsakymo aplinkybių), ir tokie teiginiai nelaikyti nepilnais ar reikalaujančiais patikslinimo. Tai reiškia, jog, priešingai nei šiandien, standartinio teiginio pavyzdys klasikiniu laikotarpiu buvo ne Jūrų mūšis vyksta laiko momentu T su stabilia teisingumo reikšme, bet [Dabar] vyksta jūrų mūšis su besikeičiančia teisingumo reikšme; tokia laikinę informaciją išreiškiančio teiginio samprata bus vadovaujamasi ir čia (plačiau apie tai žr. Prior 1967: 15–17; Øhrstrøm, Hasle 1995: 9).
Taisyklingomis loginėmis išraiškomis čia bus laikomi:
a) teiginiai p, q, r, ..., priklausantys atominių teiginių aibei At (pavyzdžiui, stipriai lyja lietus (q), šiuo metu vyksta jūrų mūšis7 (p) ir pan.);
b) iš atominių teiginių ir standartinių teiginių logikos operatorių (~, &, v, ⊃, ≡) sudaryti teiginiai (pavyzdžiui, stipriai lyjant lietui, jūrų mūšis nevyksta (q ⊃ ~p));
c) atominiai arba sudėtiniai teiginiai, modifikuoti A. Prioro silpnaisiais (F (bent sykį ateityje), P (bent sykį praeityje)) arba stipriaisiais (G (visada ateityje), H (visada praeityje) laikiniais operatoriais (pavyzdžiui, rytoj įvyks jūrų mūšis (Fp) arba visada ateityje bus teisinga, kad vakar lijo stiprus lietus (GPq));
d) atominiai arba sudėtiniai teiginiai, modifikuoti modaliniais galimybės (♢) ir būtinybės (□) operatoriais (pavyzdžiui, gali būti, kad rytoj įvyks jūrų mūšis (♢Fp) arba būtina, kad rytoj lis arba nelis stiprus lietus (□(Fq v ~Fq)).
Temporalinių išraiškų teisingumo sąlygos bus nusakomos remiantis adaptuota Kripke’ės modalinių teiginių semantika, susidedančia iš šių elementų:
1) struktūros S= <T, ≺>, kur T – laiko momentų aibė, o ≺ – ryšys anksčiau nei, siejantis aibės T elementus;
2) interpretacinės funkcijos v, visiems teiginiams p ∈ At priskiriančios teisingumo reikšmes teisinga (v(p)=1) arba klaidinga (v(p)=0) visais laiko momentais t ∈ T. Tokiu būdu gaunamas temporalinis modelis M = <T, ≺, v>;
3) temporalinių išraiškų teisingumo sąlygų apibrėžimo modelyje, t. y. jų vertinimo metodo. Šiame darbe aktualiausias bus išraiškų, modifikuotų silpnuoju būsimojo laiko operatoriumi F, vertinimo metodas, kuris gali skirtis priklausomai nuo kelių veiksnių:
3.1) parametrų, į kuriuos reikia atsižvelgti vertinant teiginį;
3.2) teisingumo reikšmių, kurias gali įgyti temporalinė išraiška, skaičiaus ir pobūdžio;
3.3) sąlygų, kurioms esant temporalinė išraiška, atsižvelgiant į (3.1) nurodytus parametrus, įgyja vieną iš (3.2) nurodytų teisingumo reikšmių.
Akivaizdu, kad tas pats temporalinis modelis M gali būti kaip pagrindas skirtingiems atsitiktinių teiginių apie ateitį vertinimo metodams. Siekiant kuo aiškesnio skirtingų semantinių teorijų palyginimo, jos bus pristatomos remiantis tuo pačiu modeliu – vienu modeliu bus remiamasi lyginant linijinę laiko struktūrą numatančias sistemas K3 ir Ł3, kitu – išsišakojančio laiko struktūrą numatančius okamizmą, supervaluacionizmą ir reliatyvizmą.
3. Linijinės struktūros CL semantinės interpretacijos: K3 ir Ł3
Loginiu požiūriu stipresnės ir sudėtingesnės, tačiau istoriškai ankstyvesnės yra linijinės laiko struktūros, o viena populiariausių tokių struktūrų yra žinoma CL (pagal Cocchiarella Linear, Cocchiarella 1965) pavadinimu. Šioje struktūroje aibės T elementus siejantis ryšys ≺ yra (1) tranzityvus, (2) linijinis į kairę ir (3) linijinis į dešinę:
(1) ∀x∀y∀z(((x ≺y)&(y ≺z))→(x ≺z));
(2) ∀x∀y∀z((y ≺x)&(z ≺x))→((y=z)v(y ≺z)v(z ≺y);
(3) ∀x∀y∀z((x ≺y)&(x ≺z))→((y=z)v(y ≺z)v(z ≺y) (kur x, y, z – kintamieji, žymintys skirtingus laiko momentus).
Ši struktūra, kurioje kitos laiko tėkmės savybės – tokios kaip tankumas, pirmo ar paskutinio momento (ne)turėjimas – yra nespecifikuotos8, grafiškai vaizduojama 3 schemoje.
3 schema

Tarkime, kad atominių teiginių aibę At sudaro du nariai – p ir q, o t0 – atskaitos taškas (momentas, kuriuo bus išsakomi / vertinami teiginiai9). Pagal antrajame poskyryje įvardytą etapą (2), arbitraliai parenkama, kuriais laiko momentais šie atominiai teiginiai yra teisingi, ir tokiu būdu gaunamas šis modelis M1:
v t-2 (p) = 1; v t-2 (q) = 1; v t-1 (p) = 0; v t-1 (q) = 1; v t0 (p) = 1; v t0 (q) = 1; v t1 (q) = 1;
v t1 (p) = 0
4 schema

Atsižvelgiant į šį modelį, vienintelis intuityviai priimtinas būsimojo laiko išraiškos Fp teisingumo sąlygų apibrėžimas yra šis:
vt0(Fp) = 1, jei ir tik jei v(t,p) = 1 bent vienam t’, kai t0 < t’
Remiantis šiuo vertinimo metodu, modelyje M1 teiginys Fp vertinimo momentu t0 yra klaidingas. Tačiau indeterministiniame kontekste – tokiame, kuriame neigiama, jog dabartiniu laiko momentu esama veiksnių, leidžiančių daryti išvadas apie dalykų padėtį vėlesniu laiko momentu – 3 schemoje pateiktas laiko tėkmės modelis atrodo sunkiai pritaikomas: čia paprasčiausiai nesama motyvo priskirti reikšmę teisinga arba klaidinga atsitiktiniams teiginiams laiko momentais, vėlesniais nei t0, mat įvykių, į kuriuos nurodo šie teiginiai, (ne)įvykimas yra dar nenuspręstas. Siekiant išlaikyti ir linijinę laiko struktūrą, ir nedeterministines pažiūras, kur kas adekvatesnis atrodo šis modelis M2:
v t-2 (p) = 1; v t-2 (q) = 1; v t-1 (p) = 0; v t-1 (q) = 1; v t0 (p) = 1; v t0 (q) = 1; v t1 (q) = ?;
v t1 (p) = ?
5 schema
Kokia tokiu atveju momentu t0 yra išraiškos Fp teisingumo reikšmė? Į šį klausimą vienodas atsakymas pateikiamas dviejose linijine struktūra paremtose semantinėse teorijose – J. Łukasiewicziaus Ł3 ir S. C. Kleene’o K3: čia, dalykų padėčiai laiko momentu t1 esant neapibrėžtai, išraiškai Fp laiko momentu suteikiamas įvertis ½, funkcionuojantis kaip trečia teisingumo reikšmė greta teisinga ir klaidinga. Formaliai išraiškos Fp teisingumo sąlygos čia gali būti nusakytos taip:
Ł/Kt0(Fp) = 1, jei ir tik jei Ł/Kt(t,p) = 1 bent vienam t, kai t0 < t
Ł/Kt0(Fp) = 0, jei ir tik jei Ł/Kt(t,p) = 0 visiems t, kai t0 < t
kitu atveju Ł/Kt0(Fp) = ½
Akivaizdu, jog, remiantis tokiu vertinimo metodu, modelyje M2 vertinimo momentu t0 reikšmę ½ įgyja ir Fp priešinga išraiška F~p10. Tai sistemose Ł3 ir K3 veda į pirmą nepageidaujamą pasekmę: kadangi tuo pačiu laiko momentu nėra teisingas nei Fp, nei F~p, nebegalioja negalimo trečiojo dėsnis (žr. 6 schemą).
6 schema
|
Kleene K3 |
Łukasiewicz Ł3 |
||||||
|
⊃ |
0 |
½ |
1 |
⊃ |
0 |
½ |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
½ |
½ |
½ |
1 |
½ |
½ |
1 |
1 |
|
1 |
0 |
½ |
1 |
1 |
0 |
½ |
1 |
|
∨ |
0 |
½ |
1 |
∨ |
0 |
½ |
1 |
|
0 |
0 |
½ |
1 |
0 |
0 |
½ |
1 |
|
½ |
½ |
½ |
1 |
½ |
½ |
½ |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Kaip matyti iš šių teisingumo lentelių, negalimo trečiojo dėsnio negaliojimas nėra vienintelis nepageidaujamas šių trireikšmių sistemų bruožas. Pagrindinis Ł3 ir K3 sistemų skirtumas – reikšmė implikacijos, sudarytos iš narių, turinčių reikšmes ½. Jei Ł3 teiginys „Jei rytoj įvyks jūrų mūšis, tai rytoj įvyks jūrų mūšis“ (Fp ⊃ Fp) turi reikšmę teisinga, tai K3 šio teiginio, atrodančio tarsi tautologija, įvertis yra ½.
Nei Ł3, nei K3 sistemose nėra įtikinamo būdo pagrįsti retrospektyvaus atsitiktinių teiginių apie ateitį vertinimo: šiose sistemose nesama priemonių, kurios leistų paaiškinti, kaip teiginys Fp, turintis reikšmę ½ laiko momentu t0, gali turėti reikšmę 1 arba 0 atsidūręs būtojo laiko operatoriaus galiojimo srityje laiko momentu t1 (t. y. tada, kai laiko momentu t1 sakoma, kad P(Fp)). Kaip bus matyti, šiuo trūkumu pasižymės visos semantinės teorijos, kuriose teisingumo reikšmė priskiriama vien tik teiginio ir vertinimo momento porai bei nėra įtraukiami papildomi parametrai.
4. Išsišakojančio laiko struktūros Kb semantinės interpretacijos: okamizmas, supervaluacionizmas ir reliatyvizmas
Ribotos linijinių struktūrų raiškos galimybės skatino temporalinės logikos tyrėjus ieškoti alternatyvių laiko tėkmės vaizdavimo būdų11. Viena tokių struktūrų, šiandien temporalinės logikos srityje jau tapusi standartine12, yra išsišakojančio laiko (branching-time) struktūra, žinoma Kb pavadinimu (pagal Kripke Branching). Šios struktūros, nors ir konceptualiai sudėtingesnės už ką tik aptartą linijinę, ryšiui ≺ keliama mažiau reikalavimų: čia apsiribojama tuo, jog jis yra (1) tranzityvus ir (2) linijinis į kairę, o dešinėje pusėje paliekama išsišakojimo galimybė13 (žr. 7 schemą).
7 schema
Arbitraliai parinkus, kuriais laiko momentais atominių teiginių aibei priklausantys teiginiai p ir q yra teisingi, gaunamas modelis M3:
v t-2 (p) = 1; v t-2 (q) = 1; v t-1 (p) = 0; v t-1 (q) = 1; v t0 (p) = 1; v t0 (q) = 1; v t1 (q) = 1;
v t1 (p) = 1, v t2 (q) = 1; v t2 (p) = 0; v t3 (q) = 0; v t3 (p) = 1; v t4 (q) = 1; v t4 (p) = 0
8 schema
Akivaizdu, jog bet kuri išsišakojančio laiko struktūra paremta semantinė teorija turi pranašumą linijine struktūra paremtų teorijų atžvilgiu dėl didesnių raiškos galimybių – kelių skirtingų ateities šakų buvimas daro teiginį ♢Fp & ♢F~p (kai abu F operatoriai nurodo į ateities momentus, vienodai nutolusius nuo dabarties momento) išpildomą14.
Naudojant išsišakojančio laiko struktūrą, esminis tampa klausimas, kokios yra išraiškos Fp teisingumo sąlygos. Matyti, jog teisingumo sąlygos, taikytos linijinei laiko struktūrai, čia nebetinka:
vt0(Fp) = 1, jei ir tik jei v(t,p) = 1 bent vienam t, kai t0 < t
To paties vertinimo metodo taikymas išsišakojančio laiko struktūroje vestų į absurdišką situaciją: čia sykiu taptų išpildomos tokios tarpusavyje nesuderinamos išraiškos kaip F(p&q)15, F~p ir F~q: modelyje M3 visos šios išraiškos taptų teisingos vertinimo momentu t0 (daugiau apie tai žr. Thomason 1970: 266–267).
Tai, jog intuityviai priimtinas būsimojo laiko operatoriaus F teisingumo sąlygų apibrėžimas veda į tokias nepageidaujamas pasekmes, kai kuriems modalinės ir temporalinės logikos tyrėjams buvo priežastis apskritai atmesti išsišakojančio laiko modelį16. Tačiau šios situacijos išvengti galima ir ne tokiais kraštutiniais būdais: toliau bus nagrinėjamos trys strategijos, kaip išsišakojančio laiko modelyje būsimojo laiko teiginių teisingumo sąlygos apibrėžiamos įtraukiant į jas papildomus parametrus.
4.1. A. Prioro okamizmas
Kartu su pirmąja formalia išsišakojančio laiko modelio formuluote 1967 m. studijoje A. Prioras pateikė ir dvi konkuruojančias šio modelio semantines interpretacijas, kurias įvardijo kaip Peirce’o17 ir okamistinę18 sistemas. Peirce’o sistema, išsitenkanti dvireikšmėje logikoje ir visus atsitiktinius teiginius apie ateitį paverčianti klaidingais, nepakliūva į šio straipsnio ribas ir čia plačiau nagrinėjama nebus.
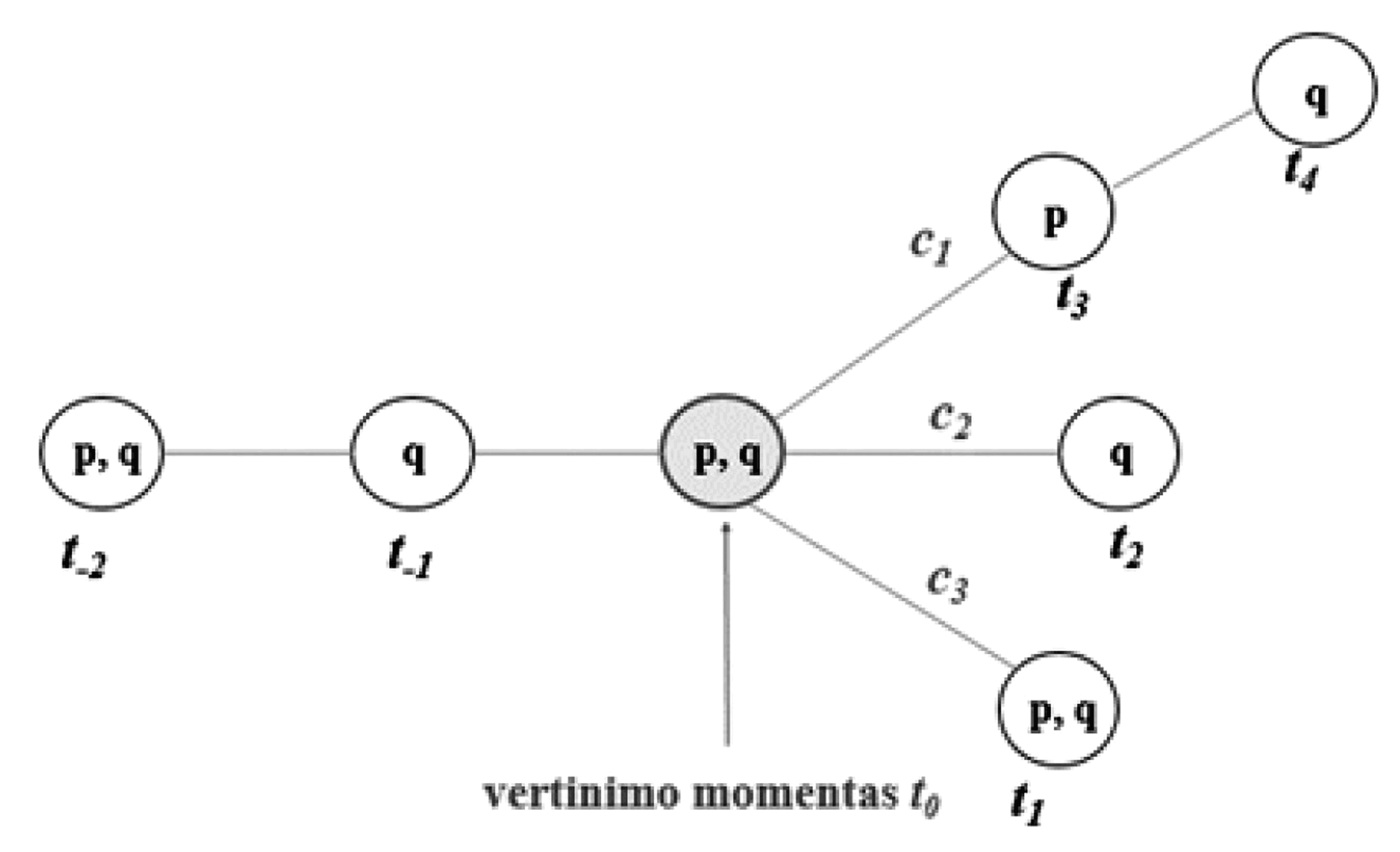
Esminis okamistinės sistemos bruožas yra tas, jog į teiginio teisingumo sąlygas čia įtraukiamas papildomas parametras c, žymintis istoriją arba kroniką, kurios 8 schemoje pažymėtos kaip c1, c2 ir c3. Istorijos arba kronikos – tai maksimalios linijine tvarka išdėstytos laiko momentų aibės, sutampančios iki laiko momento t0 ir vėliau išsiskiriančios (c1 = (t-2, t-1, t0, t3, t4), c2 = (t-2, t-1, t0, t2), c3 = (t-2, t-1, t0, t1). Taigi, atsitiktinio teiginio apie ateitį Fp teisingumo sąlygos čia yra tokios:
Ock(t,c,Fp) = 1, jei ir tik jei Ock(t′,c,p) = 1 bent vienam t′ ∈ c, kai t < t′
Ock(t,c,Fp) = 0, jei ir tik jei Ock(t′,c,p) = 0 visiems t′ ∈ c, kai t < t′
Matyti, jog, priešingai negu linijine struktūra paremtose teorijose, kur temporalinės išraiškos teisingumas priklauso tik nuo vertinimo momento (t. y. išraiškos Fp teisingumo reikšmė kinta priklausomai nuo to, kuris iš laiko momentų t ∈ T parenkamas kaip atskaitos taškas), okamizme jis priklauso ir nuo to, kurios iš galimų istorijų atžvilgiu teiginys yra vertinamas. Pavyzdžiui, modelyje M3 teiginys Fp yra teisingas vertinimo momentu t0 atsižvelgiant į istorijas c1 ir c3, tačiau klaidingas, jei į vertinimo parametrus įtraukiama istorija c2.
Okamistinėje sistemoje einama teisinga linkme siekiant išvengti ketvirtajame poskyryje aprašyto paradokso, kai tarpusavyje nesuderinamos išraiškos tuo pačiu laiko momentu gali tapti teisingos, tačiau pagrindinė problema čia lieka neišspręsta – kurios iš daugelio istorijų / ateities linijų atžvilgiu turėtume vertinti atsitiktinius teiginius apie ateitį? Klausimas, ar indeterministiniame kontekste apskritai įmanoma kalbėti apie vieną privilegijuotą ateities liniją, kurios atžvilgiu būtų vertinami atsitiktiniai teiginiai apie ateitį, yra didžiulės kontroversijos objektas (argumentus už žr. Borghini, Torrengo 2013: 123 ir toliau, argumentus prieš – Belnap et al. 2001). Prioro okamizme į šį klausimą atsakoma neigiamai: pripažįstant, jog dabartinėje dalykų padėtyje nesama nieko, kas leistų (bent iš principo) apskaičiuoti vėlesnę įvykių padėtį, vienos ateities linijos išskyrimas vertinamas kaip nesuderinamas su pačia indeterminizmo idėja (Prior, op. cit., 126–127). Dėl šios priežasties teiginiai, turintys formą Fp arba F~p, čia nėra nei teisingi, nei klaidingi – taigi, dėl tų pačių priežasčių kaip ir sistemose Ł3 bei K3 čia negalioja negalimo trečiojo dėsnis. Nors ir ekspresyvesnė už Ł3 bei K3, okamistinė sistema vis dar neteikia galimybių retrospektyviam teiginių vertinimui pagrįsti bei nepaaiškina, kokiu būdu žvelgiant iš kito vertinimo taško teiginys Fp įgyja apibrėžtą teisingumo reikšmę.
4.2. R. Thomasono supervaluacionizmas
R. Thomasono aštuntajame dešimtmetyje pasiūlyta supervaluacionistinė semantinė teorija buvo sukurta siekiant išvengti pagrindinių ligtoliniuose atsitiktinių teiginių apie ateitį problemos sprendimuose kylančių anomalijų (Thomason, op. cit.)19. Išskirtinis šios teorijos bruožas – tai, jog joje teiginio teisingumas arba klaidingumas nusakomi atsižvelgiant į tai, kokia dalykų padėtis yra visose ateities šakose:
Thom(t,Fp) = 1, jei ir tik jei Thom(t′,p) = 1 visoms c, kur t ∈ c, bent vienam t′ ∈ c, kai t < t′;
Thom(t,Fp) = 0, jei ir tik jei Thom(t′,p) = 0 visoms c, kur t ∈ c, visiems t′ ∈ c, kai t < t′;
kitu atveju Thom(t,Fp) lieka neapibrėžtas.
T. y. teiginys Fp laiko momentu t čia teisingas tada ir tik tada, jei įvykis p vėlesniu už t laiko momentu įvyksta visose galimose ateities įvykių eigose (ir atitinkamai: klaidingas – jei neįvyksta nė vienoje jų). Akivaizdu, jog nė vienas atsitiktinis teiginys tokių sąlygų netenkina – teiginiai, esantys teisingi visose galimose ateities linijose, yra ne atsitiktiniai, o būtini (ir atitinkamai: teiginiai, klaidingi visose galimose ateities linijose, yra ne atsitiktiniai, o neįmanomi). Pažvelgus į modelį M3, matyti, jog, taikant supervaluacionistinius Thomasono teisingumo kriterijus, teiginys Fp vertinimo momentu t0 nėra nei teisingas, nei klaidingas – istorijoje c2 įvykių padėties p nėra.
Didelis Thomasono teorijos privalumas lig šiol nagrinėtų teorijų atžvilgiu yra tas, jog nepaisant fakto, kad nei Fp, nei F~p vertinimo momentu t0 nėra nei teisingi, nei klaidingi, jų disjunkcija Fp v F~p vertinimo momentu t0 yra teisinga – tai reiškia, kad išsaugomas negalimo trečiojo dėsnis. Šio rezultato pasiekiama kiek liberaliau traktuojant įprastas teisingumo lentelių technikas. Pagal standartines klasikinės logikos teisingumo lenteles, disjunkcija yra teisinga, jei ir tik jei yra teisingas bent vienas jos narių, o supervaluacionistinėje semantikoje disjunkcija Fp v F~p gali būti teisinga ir tada, kai reikšmės teisinga neturi nė vienas iš ją sudarančių narių. Kaip jau buvo minėta, remiantis supervaluacionistiniais teisingumo kriterijais ir vadovaujantis 8 schema, vertinimo momentu t0 ir teiginys Fp, ir teiginys F~p pasižymi teisingumo reikšmės pertrūkiu: žvelgiant iš laiko momento t0, teiginys Fp yra teisingas c1 istorijos atžvilgiu, klaidingas c2 istorijos atžvilgiu ir teisingas c3 istorijos atžvilgiu, todėl absoliučia prasme (neatsižvelgiant į konkrečią istoriją) neturi jokios teisingumo reikšmės. Kitaip yra su disjunkcija Fp v F~p: žvelgiant iš laiko momento t0, toks teiginys yra teisingas ir c1 bei c3 istorijų atžvilgiu (nes jų atžvilgiu teisingas teiginys Fp), ir c2 istorijos atžvilgiu (nes jos atžvilgiu teisingas teiginys F~p) – vadinasi, teiginys Fp v F~p vertinimo momentu t0 čia yra teisingas ir absoliučia prasme.
Taigi, Thomasono supervaluacionizmas lenkia lig šiol nagrinėtas teorijas bent pora aspektų – šioje teorijoje, besiremiančioje išsišakojančio laiko struktūra, sudaromos galimybės išraiškai ♢Fp & ♢F~p būti teisingai; čia taip pat išsaugomas negalimo trečiojo dėsnis. Deja, čia, kaip ir ankstesnėse teorijose, vis dar nėra techninių galimybių parodyti, kokiu būdu teiginiui Fp, vertinamam atgaline data, gali būti priskiriama tradicinė teisingumo reikšmė teisinga arba klaidinga.
4.3. J. MacFarlane’o reliatyvizmas
J. MacFarlane’o reliatyvistinė semantinė teorija (MacFarlane 2003) buvo sukurta siekiant pašalinti visoms iki šiol nagrinėtoms teorijoms būdingą trūkumą – negebėjimą suderinti neapibrėžtumo intuicijos, pagal kurią atsitiktiniai teiginiai apie ateitį, vertinami iš dabarties taško, nėra nei teisingi, nei klaidingi (t. y. įsitikinimo, jog šiandien išsakomas teiginys „Rytoj įvyks jūrų mūšis“ neturi jokios teisingumo reikšmės), ir apibrėžtumo intuicijos, kai tie patys teiginiai vertinami jau (ne)įvykus atitinkamiems įvykiams (t. y. manymo, jog jau įvykus jūrų mūšiui pagrįsta sakyti, kad asmuo, vakar išsakęs teiginį „Rytoj įvyks jūrų mūšis“, buvo teisus).
Galimybę šioms dviem intuicijoms egzistuoti drauge MacFarlane’as sudaro įvesdamas į būsimojo laiko teiginių teisingumo sąlygas papildomą parametrą – greta vertinimo momento t ir istorijos c čia atsiranda vertinimo kontekstas (context of assessment) a. Pasak MacFarlane’o, pagrindinė ankstesniųjų semantinių teorijų yda yra įsitikinimas, jog temporalinių išraiškų reikšmė yra absoliuti – t. y. nepriklausanti nuo teiginio vertinimo aplinkybių. Remiantis reliatyvistinėmis nuostatomis, į modelį M3 įtraukiami trys skirtingi vertinimo kontekstai – a1, a2 ir a3 (siekiant aiškumo, parametras t čia pervadintas teiginio išsakymo momentu) (žr. 9 schemą).
9 schema
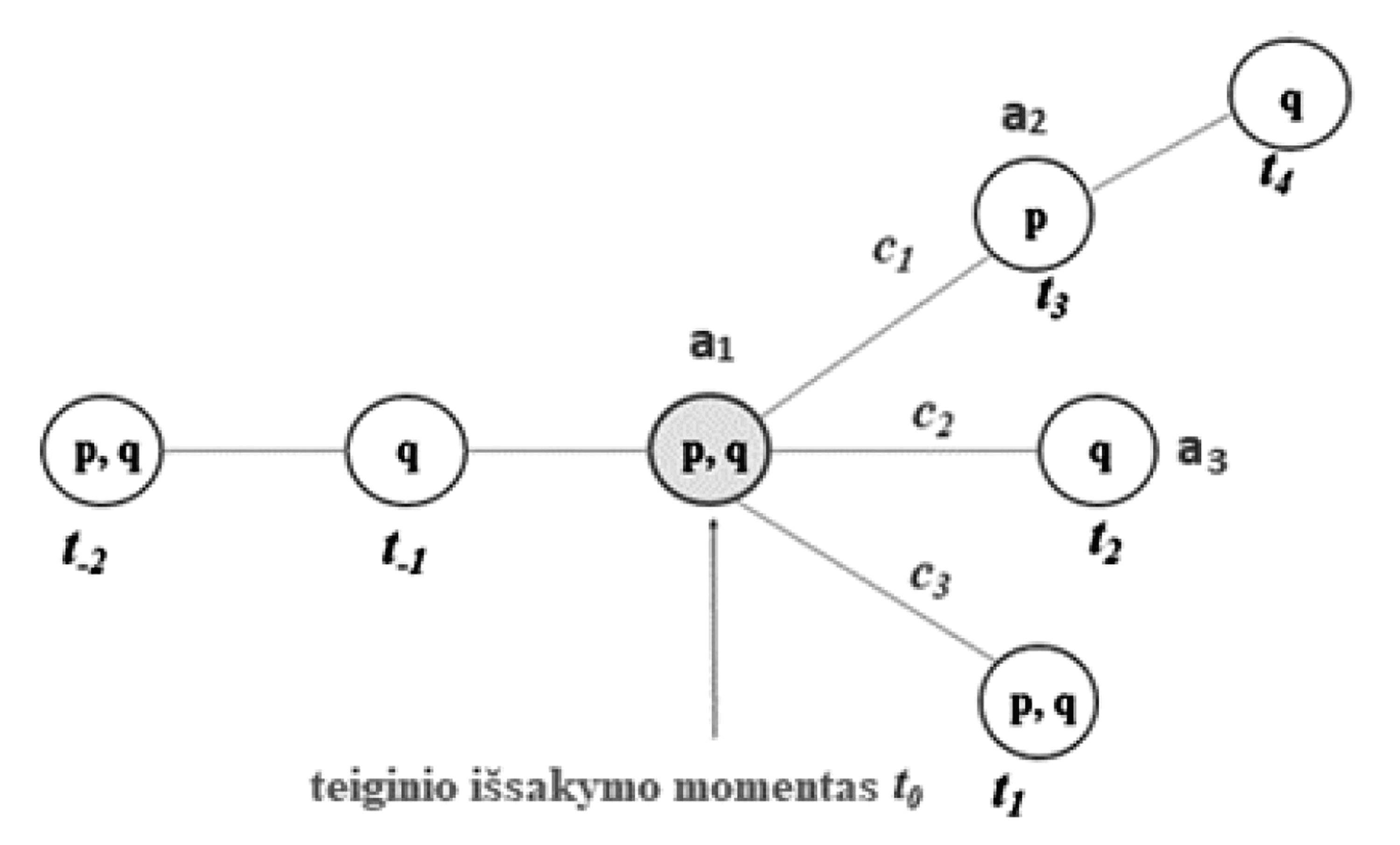
Jei teiginio išsakymo momentas t ir teiginio vertinimo kontekstas a sutampa, teiginio Fp vertinimas šiame modelyje atrodo labai panašiai kaip supervaluacionizme:
Jei ir tik jei a=t:
MacF(t,a,Fp) = 1, jei ir tik jei MacF(t′,p) = 1 visoms c, kur t ∈ c, bent vienam t′ ∈ c, kai t < t′;
MacF(t,a,Fp) = 0, jei ir tik jei MacF(t′,p) = 0 visiems t′ ∈ c, visoms c, kur t ∈ c, kai t < t′;
kitu atveju MacF(t,a,Fp) lieka neapibrėžtas.
Taigi, čia teiginys Fp, išsakytas momentu t0 ir vertinamas kontekste a1, neturi jokios teisingumo reikšmės, mat istorijose c1, c2 ir c3 vėlesniu už t0 momentu t teiginys p turi skirtingas reikšmes. Tačiau jei teiginio vertinimo momentas a yra vėlesnis už teiginio išsakymo momentą t (t. y. t ≺a), Fp teisingumo sąlygos yra šios:
Jei ir tik jei t ≺a:
MacF(t,a,Fp) = 1, jei ir tik jei MacF(t′,p) = 1 bent vienam t′ ∈ c, kai t < t′, visoms c, kur t, a ∈ c;
MacF(t,a,Fp) = 0, jei ir tik jei MacF(t′,p) = 0 visiems t′ ∈ c, kai t < t′, visoms c, kur t, a ∈ c
Matyti, jog tada, kai vertinimo kontekstas nusikelia į vėlesnį laiką (pavyzdžiui, a2), pakanka, jog p teisingas tik toje istorijoje (šiuo atveju – c1), kuriai priklauso vertinimo kontekstas.
Taigi, jei Fp reiškia „Rytoj įvyks jūrų mūšis“, reliatyvizme šio teiginio reikšmė atrodo taip (pagal 9 schemą):
1) teiginys Fp yra nei teisingas, nei klaidingas, jei teiginio išsakymo momentas yra t0, o vertinimo kontekstas yra a1;
2) teiginys Fp yra teisingas, jei teiginio išsakymo momentas yra t0, o vertinimo kontekstas yra a2;
3) teiginys Fp yra klaidingas, jei teiginio išsakymo momentas yra t0, o vertinimo kontekstas yra a3.
Reliatyvistinėje teorijoje ne tik išsprendžiama retrospektyvaus teiginių vertinimo problema – čia taip pat išlaikomas ir negalimo trečiojo dėsnis: kaip ir supervaluacionizme, teiginys Fp v F~p laiko momentu t0 čia yra teisingas visų galimų ateities linijų atžvilgiu visuose vertinimo kontekstuose. Be to, joje, paremtoje išsišakojančio laiko struktūra, yra išpildoma išraiška ♢Fp & ♢F~p. Kol kas ši teorija atrodo konkurencingiausia sprendžiant atsitiktinių teiginių apie ateitį problemą, tačiau kitame skyriuje bus aptarti dar keli iššūkiai, kurie kelia sunkumų visoms penkioms šiame darbe nagrinėtoms semantinėms teorijoms.
5. Tradicinių teisingumo reikšmių pertrūkiai ir dieviškoji visažinystė: teologinio fatalizmo įrodymas
Atsitiktinių teiginių apie ateitį problema ne visada buvo svarstoma loginiame kontekste – nemažai įtakingų šios problemos sprendimų buvo pasiūlyta sprendžiant teologinę jos formuluotę: klausimą, ar ir kaip apibrėžtos teisingumo reikšmės turėjimas suderinamas su atviros ateities intuicija, atitinka klausimas, kaip šią atviros ateities intuiciją galima suderinti su idealaus pažįstančiojo subjekto, kuriam yra žinomi visi teiginiai apie praeitį, dabartį ir ateitį, egzistavimu.
Bet kurioje episteminės logikos sistemoje galioja ši visai nekontroversiška implikacija, tesakanti tai, kad jei agentas A žino teiginį p, tai teiginys p yra teisingas (kitaip sakant, žinoti galima tik teisingus teiginius – jei teiginys p nėra teisingas, jo atžvilgiu galima tik silpnesnė (pavyzdžiui, manymo ar tikėjimo) episteminė nuostata):
KA p ⊃ p
Priėmę prielaidą, jog egzistuoja idealus pažįstantysis subjektas D, jo atžvilgiu turime priimti abipusę implikaciją, arba ekvivalenciją, sakančią ne tik tai, jog, jei agentas D žino teiginį p, tai teiginys p yra teisingas, bet ir tai, jog, jei teiginys p yra teisingas, tai agentas D jį žino:
KD p ≡ p
Ši ekvivalencija leidžia performuluoti pirmajame darbo skyriuje pateiktą samprotavimą taip:
1. Egzistuoja esybė, žinanti visus teiginius apie praeitį, dabartį ir ateitį;
2. Ši esybė žino teiginį, jei ir tik jei egzistuoja jį atitinkanti dalykų padėtis;
3. Ši esybė teiginio nežino, jei ir tik jei egzistuoja jam priešinga dalykų padėtis;
∴ Jau dabar egzistuoja apibrėžta viena būsimų įvykių eiga.
Tradicinių teisingumo reikšmių pertrūkiai kelia akivaizdžių problemų svarstant teologinę atsitiktinių teiginių apie ateitį problemos versiją. Priimdami ekvivalenciją KDFp ≡ Fp, privalėtume sutikti, jog teiginys „Visažinė būtybė žino, kad Fp“ čia nėra teisingas, kai p – atsitiktinis teiginys. Akivaizdu, jog visose aptartose teorijose, kuriose negalioja negalimo trečiojo dėsnis (Ł3, K3 ir okamizme), teisingas nėra ir jam ekvivalentiškas teiginys KDFp v KD~Fp, tesakantis tik tai, jog arba visažinė būtybė D žino, kad įvyks p, arba visažinė būtybė žino, kad p neįvyks. Tačiau tai, jog tokie teiginiai nėra teisingi, atrodo sunkiai suderinama su pačios visažinės būtybės egzistavimu.
Paradoksalią situaciją, kai teiginiai KDFp, KD~Fp ir KDFp v KD~Fp nėra teisingi, galima bandyti pateisinti bent pora būdų:
1) išpažįstant vieną iš metafizinių teorijų, atmetančių realų ateities įvykių bei objektų egzistavimą (pavyzdžiui, prezentizmą (presentism), kuriame griežta prasme egzistuoja tik dabartis, arba augančios visatos teoriją (growing block theory), kur realumo statusas suteikiamas tik tam, kas buvo, ir tam, kas yra), ir teigiant, kad Fp formą turintys teiginiai, nurodantys į neegzistuojančius objektus arba įvykius, apskritai nėra prasmingi ir todėl negali būti dieviškojo pažinimo domeno dalis;
2) pasinaudojant viduramžiais populiaria strategija ir teigiant, jog idealus pažįstantysis subjektas, arba Dievas, apskritai nėra laike (tokios pozicijos laikėsi, pavyzdžiui, Boecijus ir Tomas Akvinietis), todėl tada, kai pažinimo agentas yra D, išraiškos su laikiniais operatoriais negali pakliūti į episteminio operatoriaus K sritį.
Deja, net jei šią nepageidaujamą situaciją ir būtų galima išspręsti vienu iš pasiūlytų būdų, tradicinių teisingumo reikšmių pertrūkių egzistavimas palieka kitų problemų svarstant visažinystės ir atviros ateities santykio problemą.
Viena tokių problemų buvo suformuluota visai neseniai (žr. Todd, Rabern 2019) ir įtikinamo sprendimo jai kol kas nerasta – bus matyti, jog ji ypač aktuali MacFarlane’o reliatyvizme, visais kitais atžvilgiais lenkiančiame kitas nagrinėtas semantines teorijas. Aptariama problema kyla svarstant retrospektyvaus atsitiktinių teiginių apie ateitį vertinimo galimybę teologiniame kontekste. Atsižvelgiant į šias intuityviai priimtinas ekvivalencijas (pagal Todd, Rabern, op. cit., p. 9):
p ≡ KDp (p, jei ir tik jei visažinė būtybė / idealus pažįstantysis subjektas D žino, kad p)
Fp ≡ AntDp (bent sykį ateityje bus p, jei ir tik jei visažinė būtybė / idealus pažįstantysis subjektas D anticipuoja / iš anksto žino (Ant), kad p)
Pp ≡ RemDp (bent sykį praeityje buvo p, jei ir tik jei visažinė būtybė / idealus pažįstantysis subjektas D atsimena (Rem), kad p)
– teiginio p ⊃ PFp atitikmuo teologiniame kontekste yra p ⊃ RemD(AntDp). Net ir MacFarlane’o reliatyvizme, kuriame išraiška p ⊃ PFp nekelia didesnių problemų, sudėtinga atsakyti, kokiu būdu galima suderinti šias dvi nuostatas (atsižvelgiant į modelį M3):
1) netiesa, jog visažinė būtybė laiko momentu t0 žino, kad Fp;
2) visažinė būtybė laiko momentu t3 atsimena, kad laiko momentu t0 anticipavo / iš anksto žinojo, kad p.
Atrodo, jog perėjimą nuo teiginio „Netiesa, jog visažinė būtybė laiko momentu t0 žino, kad Fp“ prie teiginio „Visažinė būtybė laiko momentu t0 žinojo, kad Fp“ paaiškinti kur kas sudėtingiau nei perėjimą nuo teiginio „Ištara Fp nėra teisinga laiko momentu t0“ prie teiginio „Ištara Fp buvo teisinga laiko momentu t0“. Nuo to, ar ir kaip galima suderinti šias dvi priešingas idealaus pažįstančiojo subjekto nuostatas tos pačios dalykų padėties atžvilgiu, priklauso MacFarlane’o reliatyvistinės teorijos sėkmė.
6. Apibendrinimas ir tolesnio darbo perspektyvos
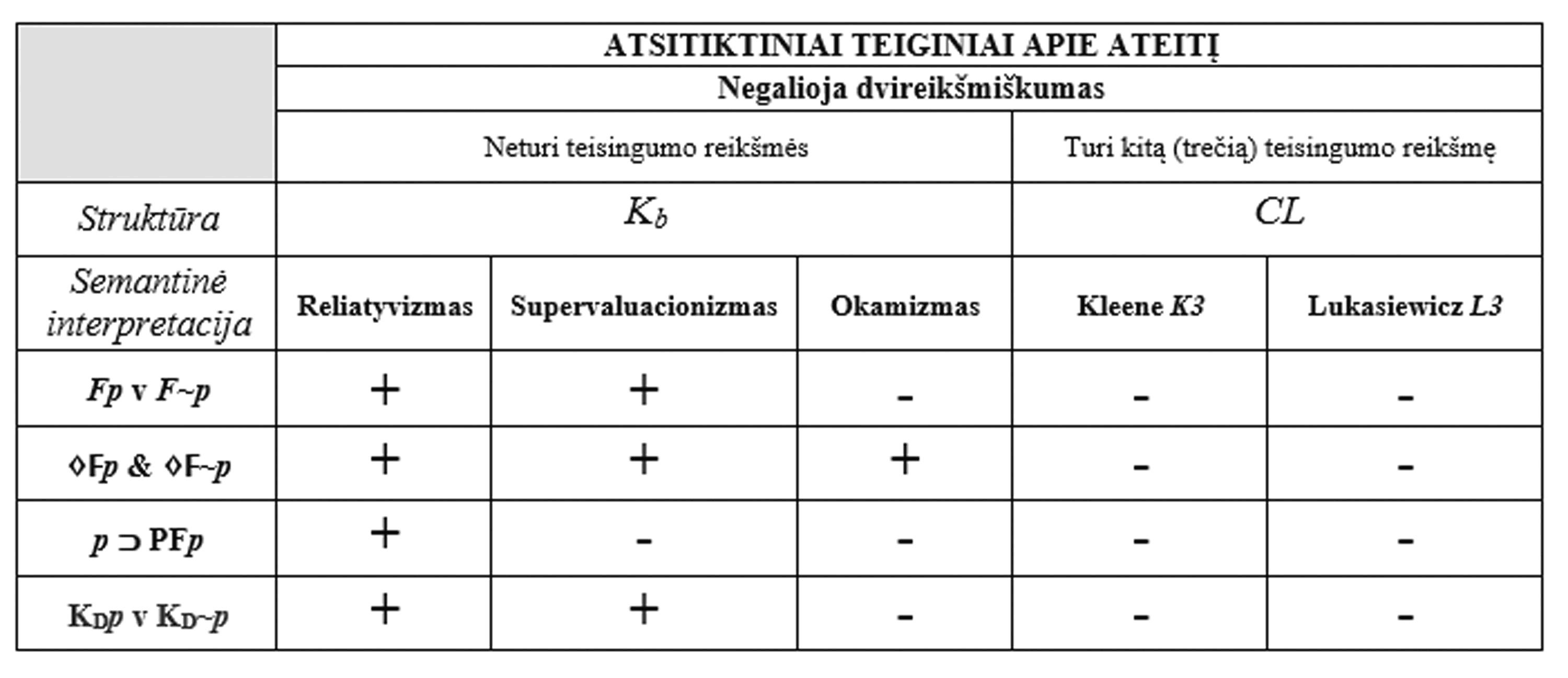
Šiame darbe aptartos penkios semantinės teorijos, atsitiktinių teiginių apie ateitį problemos sprendimų tradicijoje atstovaujančios semantinio inkompatibilizmo pozicijai. Atlikus jų analizę, gauta ši išsami tipologija (žr. 10 schemą).
1. Ł3, K3 ir okamistinę sistemas vienijantis trūkumas – negalimo trečiojo dėsnio negaliojimas: čia išraiška Fp v F~p, kai p – atsitiktinis teiginys, turi reikšmę ½; be to, nė viena šių sistemų negeba pagrįsti retrospektyvaus atsitiktinių teiginių vertinimo. Okamistinė teorija Ł3 ir K3 atžvilgiu išlieka pranašesnė dėl didesnių raiškos galimybių – joje, paremtoje išsišakojančio laiko struktūra, išpildoma tampa išraiška ♢Fp & ♢F~p.
2. Negalimo trečiojo dėsnis išlaikomas supervaluacionistinėje ir reliatyvistinėje semantinėse teorijose – jose, paremtose išsišakojančio laiko struktūra, išraiška ♢Fp & ♢F~p taip pat yra išpildoma).
3. Tik reliatyvistinėje teorijoje esama būdų pagrįsti retrospektyvų atsitiktinių teiginių apie ateitį vertinimą: čia, įvedus papildomą parametrą, paaiškinama, kokiu būdu teiginys Fp gali įgyti skirtingas reikšmes atsižvelgiant į skirtingą vertinimo kontekstą.
4. Nė viena iš nagrinėtų teorijų nėra adekvati nagrinėjant teologinę-epistemologinę atsitiktinių teiginių apie ateitį problemos formuluotę, įtraukiančią idealų pažįstantįjį agentą: visose iš nagrinėtų teorijų teiginiai KDp ir KD~p nėra nei teisingi, nei klaidingi, o tose, kuriose neišsaugomas negalimo trečiojo dėsnis, teisingas nėra nei dar trivialesnis teiginys (KDp v KD~p). Reliatyvistinėje teorijoje kyla rimtų sunkumų paaiškinant, kokiu būdu gali būti suderinami teiginiai „Netiesa, jog visažinė būtybė laiko momentu t0 žino, kad Fp“ ir „Visažinė būtybė laiko momentu t0 žinojo, kad Fp“.
10 schema
Atsižvelgiant į pateiktus analizės rezultatus, sprendžiant atsitiktinių teiginių apie ateitį problemą galimi šie tolesni veiksmai:
1) sekti pastarųjų metų mėginimais modifikuoti teorijas su tradicinių teisingumo reikšmių pertrūkiais taip, jog jose liktų kuo mažiau nepageidaujamų pasekmių: pavyzdžiui, neseniai būta mėginimų pakeisti Ł3 sistemą taip, jog šioje būtų išlaikomas negalimo trečiojo dėsnis – vienas žymiausių tokių bandymų paremtas neigimo apibrėžimo Ł3 sistemoje pakeitimu (žr. Akama et al. 2007);
2) rinktis dvireikšmėje logikoje išsitenkančius atsitiktinių teiginių apie ateitį problemos sprendimus. Garsiausios teorijos, suteikiančios visiems Fp formą turintiems teiginiams teisingumo reikšmes teisinga arba klaidinga – tai išsišakojančio laiko struktūra paremta „plonos raudonos linijos“ (thin red line) teorija20 ir D. Lewiso „antrininkų“ (counterparts), egzistuojančių paraleliose, tarpusavyje nesusijungiančiose laiko linijose, teorija (Lewis, op. cit.). Šios dvireikšmės semantinės teorijos susiduria su visai kitokio pobūdžio iššūkiais nei čia aptartieji, tačiau jų analizė yra atskiro tyrimo objektas, nebepatenkantis į šio straipsnio ribas.
Literatūra
Akama, S., Nagata, Y. et al., 2007. A Three-Valued Temporal Logic for Future Contingents. Logique et Analyse 50 (198): 99–111. DOI: https://doi.org/10.1007/s11225-008-9102-0
Belnap, N., 2001. Double Time References: Speech-act Reports as Modalities in an Indeterminist Setting. In: Advances in Modal Logic, eds. Wolter, F. et al., vol. 3. Stanford: CSLI Publications. DOI: https://doi.org/10.1142/9789812776471_0003
Belnap, N., Perloff, M., Xu, M., 2001. Facing the Future: Agents and Choices in Our Indeterminist World. Oxford: Oxford University Press.
Benovsky, J., 2013. Branching and (in)Determinism. Philosophical Papers 42 (2): 151–173. DOI: https://doi.org/10.1080/05568641.2013.806286
Borghini, A., Torrengo, G., 2013. The Metaphysics of the Thin Red Line. In: Around the Tree, eds. F. Correia and A. Iacona, A., Synthese Library vol. 361, 105–127. DOI: https://doi.org/10.1007/978-94-007-5167-5_7
Cocchiarella, N. B., 1965. Tense and Modal Logic: A Study in the Topology of Temporal Reference (Ph. D. thesis, University of California at Los Angeles).
Łukasiewicz, J., 1970. Selected Works. L. Borkowski (Ed.). London, UK: North-Holland Publishing Company.
Kamp, H., 1968. Tense Logic and the Theory of Linear Order (Ph.D. thesis). University of California, Los Angeles.
Kripke, S. A., 1959. A Completeness Theorem in Modal Logic. Journal of Symbolic Logic 24 (1): 1–14. DOI: https://doi.org/10.2307/2964568
Kripke, S. A., 1963. Semantical Analysis of Modal Logic I. Normal Propositional Calculi. Zeitschrift fur mathematische Logik und Grundlagen der Mathematik 9 (5–6): 67–96. DOI: https://doi.org/10.1002/malq.19630090502
Lewis, D. K., 1973. Counterfactuals. Blackwell & Harvard University Press.
MacFarlane, J., 2003. Future Contingents and Relative Truth. The Philosophical Quarterly 53 (212): 321–36. DOI: https://doi.org/10.1111/1467-9213.00315
Øhrstrøm, P., 1981. Problems Regarding the Future Operator in an Indeterministic Tense Logic. Danish Yearbook of Philosophy 18: 91–95.
Øhrstrøm, P., Hasle, P., 1995. Temporal Logic: from Ancient Ideas to Artificial Intelligence. Dordrecht: Kluwer Academic Publishers. DOI: https://doi.org/10.2307/2275590
Pnueli, A., 1977. The Temporal Logic of Programs. Proceedings of the 18th IEEE Symposium on Foundations of Computer Science, 46–67.
Prior, A. N., 1957. Time and Modality. Oxford: Clarendon Press.
Prior, A. N., 1967. Past, Present and Future. Oxford: Clarendon Press.
Rosenkranz, S., 2013. Determinism, Open Future, and Branching Time. In: Around the Tree: Semantic and Metaphysical Issues Concerning Branching and the Open Future, eds. F. Correia, F. and A. Iacona, A., Synthese Library vol. 361, 47–72. Dordrecht: Springer. DOI: https://doi.org/10.1007/978-94-007-5167-5_3
Thomason, R. H., 1970. Indeterminist Time and Truth Value Gaps. Theoria 36: 264–281. DOI: https://doi.org/10.1111/j.1755-2567.1970.tb00427.x
Todd, P., Rabern, B., 2019. Future Contingents and the Logic of Temporal Omniscience. Noûs 0 (0): 1–26. DOI: https://doi.org/10.1111/nous.12294
van Fraassen, B., 1968. Presupposition, Implication, and Self-Reference. Journal of Philosophy 65 (1968): 136–152. DOI: https://doi.org/10.2307/2024557
1 Šį De interpretatione devintojo skyriaus fragmentą (DI 9 18a34–18b16) įprasta įvardyti kaip jūrų mūšio „paradoksą“, tačiau, atsižvelgiant į šio darbo tikslus, šią De interpretatione ištrauką čia parankiau pateikti ne kaip kelių tarpusavyje nederančių teiginių rinkinį, o kaip samprotavimą, kuriame intuityviai priimtinos prielaidos veda į intuityviai nepriimtiną išvadą.
2 Originaliame tekste esama bent dviejų samprotavimo, vedančio į loginį fatalizmą, formuluočių:
I formuluotė (DI 9 18a34–b9):
1) kiekvienas teiginys yra teisingas arba klaidingas;
2) įmanoma, kad kas nors vienas šiandien sakytų, jog rytoj jūrų mūšis įvyks, o kitas tai neigtų;
3) pasitvirtins tik vieno iš jųdviejų spėjimas;
4) spėjimas, kuris (ne)pasitvirtins, yra teisingas (klaidingas) jau dabar;
5) jei šiandien teisinga (klaidinga), kad rytoj įvyks jūrų mūšis, tai rytoj būtinai (ne)įvyks jūrų mūšis.
II formuluotė (DI 9 18b9–16):
1) kiekvienas teiginys yra teisingas arba klaidingas;
2) jei įvykis vyksta, anksčiau buvo teisinga teigti, kad jis įvyks;
3) jei anksčiau buvo teisinga teigti, kad įvykis įvyks, jis negali nevykti;
5) jei anksčiau buvo teisinga teigti, kad įvykis įvyks, jis vyksta būtinai (pagal operatorių ekvivalenciją ~◊~ ≡ □).
Tai, jog spėjimas apie įvykio (ne)įvykimą išsakomas iki (ne)įvykstant įvykiui, yra bendras abiejų samprotavimo formuluočių bruožas. Kita vertus, antrojoje formuluotėje įvykio baigtis jau aiški, o pirmojoje – dar nežinoma. Suprasdamas, jog pirmosios formuluotės prielaida, esą į įvyksiančius įvykius nurodantys teiginiai yra teisingi jau dabar, gali būti intuityviai nepriimtina, Aristotelis pateikia alternatyvią ir patrauklesnę jos versiją antrojoje formuluotėje. Spėjimo apie būsimą įvykį data čia perkeliama iš dabarties į praeitį, o įvykio vyksmas – iš ateities į dabartį: jei įsivaizduotume, jog teiginys „Rytoj įvyks jūrų mūšis“ buvo išsakytas ne šiandien, o vakar, šiandien šiam mūšiui įvykus vakarykštį spėjimą linktume laikyti teisingu. Tokiu atveju teisingu ar klaidingu analogiškai turime laikyti ir šiandienį teiginį apie tai, kas galbūt bus rytoj – perspektyvos pasikeitimas, Aristotelio nuomone, esmės čia nekeičia.
3 Žinoma, svarstant nesutrumpintą samprotavimo versiją, susidedančią iš daugiau prielaidų, atsirastų ir daugiau jo atmetimo galimybių.
4 Paprastai, norint pasakyti, kad Fp ir Fq kalba apie įvykius, vyksiančius praėjus vienodam laiko kiekiui nuo dabarties momento, pasitelkiami metriniai temporaliniai operatoriai, pavyzdžiui, F1 0 q (skaityti – „q įvyks ateityje praėjus 10-čiai laiko vienetų nuo dabarties momento“), tačiau čia, siekiant kuo didesnio paprastumo, metriniai operatoriai nenaudojami.
5 Nuo pirmųjų temporalinei logikai skirtų Prioro darbų pasirodymo iki šių dienų buvo įvesta daug kitų laikinių operatorių, išplečiančių temporalinės logikos raiškos galimybes (pvz., S (since) ir U (until) operatoriai (Kamp 1968)), tačiau išraiškos su jais šiame straipsnyje neatliks jokio vaidmens.
6 Apie laiko intervalais paremtą temporalinę logiką, pasižyminčią didesnėmis raiškos galimybėmis, šiame darbe kalbama nebus.
7 Pagal temporalinėje logikoje įsigalėjusį standartinį požiūrį, atominiai teiginiai, nemodifikuoti jokiu laikiniu operatoriumi, yra esamojo laiko – dėl šios priežasties klasikinėje A. Prioro sintaksėje nėra išskiriamas atskiras esamojo laiko operatorius (žr. punktą (c)), kuris čia laikomas pertekliniu.
8 Išmetus iš sistemos pirmą ir paskutinį laiko momentą (t. y. specifikavus ryšį ≺ kaip, atitinkamai, ∀x∃y(y ≺x) ir ∀x∃y(x ≺y)) gaunama sistema SL (Scott Linear), o pridėjus tankumą (∀x∀y(x ≺y→∃z(x ≺z∧z ≺y)) pereinama prie dar stipresnės sistemos PL (Prior Linear).
9 Kol kas šie momentai sutampa.
10 Neigimo operatoriaus vieta šiuo atveju turi būti būtent čia, nes išraiška ~Fp yra kur kas stipresnė nei F~p: jei F~p tesako, kad ateityje bent vienu laiko momentu nebus taip, kad p, tai ~Fp teigia, kad tokio momento, kai p, ateityje nebus visai.
11 Nors linijine struktūra paremtos temporalinės logikos sistemos turi ribotą pritaikomumą filosofinėms reikmėms, jomis plačiai remiamasi informatikos moksle: ten viena populiariausių yra linijinė temporalinė logika LTL, kurioje naudojami tik trys ateities operatoriai X (next), G (always going to be) ir U (until) (plačiau žr. Pnueli 1977).
12 Su retomis išimtimis: išsišakojančio laiko modelį kaip nereikalingą komplikaciją kalbant apie atviros ateities galimybes atmeta Rosenkranz (2013), taip pat Benovsky (2013).
13 Temporalinėje logikoje išsišakojimas vyksta savaime, todėl išsišakojančio laiko struktūros apibrėžiamos per tai, ko joms trūksta (linijiškumo į kairę ir / arba į dešinę), ir tokiomis struktūromis paremtos sistemos yra silpnesnės už linijines.
14 Kur išraiška Fp vertinamuoju momentu t0 teisinga tada ir tik tada, jei p teisingas bent vienu už t0 vėlesniu laiko momentu bent vienoje istorijoje c, kuriai priklauso vertinamasis momentas t0.
15 Kai konjunkcijos teisingumo sąlygos – tos pačios kaip ir klasikinėje teiginių logikoje, t. y. čia: vt0(F(p&q)) = 1, jei ir tik jei bent vienam t, kai t0 < t, vt (p) = 1 ir vt(q) = 1.
16 Dėl to, jog nepridėjus papildomų parametrų išsišakojančio laiko modelyje per daug tarpusavyje nesuderinamų teiginių tampa teisingi, šią struktūrą atmetė Davidas Lewisas, indeterministinę visatą siūlęs vaizduoti kaip paraleliai viena kitos einančias linijas („O jei kas nors teigtų, kad rytoj įvyks jūrų mūšis – žinoma, turėdamas galvoje jo paties pasaulyje įvyksiančią ateitį, – ir kitądien viename iš pasaulių jūrų mūšis įvyktų, o kitame – ne?“ (Lewis 1973: 359–360)).
17 Taip pavadinta pagal galimas sąsajas su amerikiečių filosofo ir logiko C. S. Peirce’o (1839–1914) darbais.
18 Nors akivaizdu, kad sistemos pavadinimas sugalvotas pagal viduramžių filosofo ir logiko Viljamo Okamo vardą, konceptualinių panašumų tarp šios sistemos ir Okamo pažiūrų esama nedaug. Atsitiktinių teiginių apie ateitį problemos tyrimų lauke plačiai žinomas nemažą painiavą keliantis nesutapimas tarp istorinio Okamo požiūrio (pagal kurį visi atsitiktiniai teiginiai apie ateitį yra arba teisingi, arba klaidingi) ir to, ką Prioras vadina okamizmu (pagal kurį atsitiktiniai teiginiai apie ateitį nėra nei teisingi, nei klaidingi). Šiame darbe okamizmo terminas visur vartojamas turint galvoje Prioro okamizmą.
19 Thomasonas čia glaudžiai remiasi B. van Fraasseno idėjomis, tik pritaiko jas kitame kontekste – dar 1968 m. supervaluacionistinę semantinę teoriją van Fraassenas (1968) pasiūlė kaip būdą spręsti savireferencijos paradoksus.
20 Formaliai pirmąkart ji pristatyta Øhrstrøm 1981: 91–95.