Problemos ISSN 1392-1126 eISSN 2424-6158
2022, vol. 101, pp. 31–41 DOI: https://doi.org/10.15388/Problemos.101.3
Inferences Between Buridan’s Modal Propositions
Jonas Dagys
Institute of Philosophy
Vilnius University
Email jonas.dagys@fsf.vu.lt
ORCID https://orcid.org/0000-0001-9033-4562
Haroldas Giedra
Institute of Computer Science
Vilnius University
Email haroldas.giedra@mif.vu.lt
ORCID https://orcid.org/0000-0002-6852-5909
Živilė Pabijutaitė
Institute of Philosophy
Vilnius University
El. paštas: zivile.pabijutaite@fsf.vu.lt
ORCID https://orcid.org/0000-0002-4928-7298
Abstract. In recent years modal syllogistic provided by 14th century logician John Buridan has attracted increasing attention of historians of medieval logic. The widespread use of quantified modal logic with the apparatus of possible worlds semantics in current analytic philosophy has encouraged the investigation of the relation of Buridan’s theory of modality with the modern developments of symbolic modal logic. We focus on the semantics of and the inferential relations among the propositions that underlie Buridan’s theory of modal syllogism. First, we review all inferences between propositions of necessity, possibility, contingency, and non-contingency, with or without quod est locution, that are valid in Buridan’s semantics, and offer a comprehensive diagrammatic representation that includes them all. We then ask the question if there is a way to model those results in first order modal logic. Three ways of formalizing Buridan’s propositions in quantified modal logic are considered. Comparison of inferences between the quantified formulas and Buridan’s propositions reveals that, when supplied with a suitable formalization, Buridan’s semantics of categorical statements and immediate inferences among them can be fully captured by the quantified modal system T.
Keywords: Buridan’s logic, modal syllogistic, first order modal logic, possible worlds semantics
Išvedimai tarp Buridano modalinių teiginių
Santrauka. Straipsnyje nagrinėjama XIV a. logiko Jono Buridano modalinė logika, pastaraisiais metais sulaukianti vis didesnio viduramžių logikos tyrėjų dėmesio. Šiuolaikinėje analitinėje filosofijoje plačiai naudojama modalinė predikatų logika, paremta galimų pasaulių semantika, paskatino kelti klausimus apie Buridano modalumų teorijos ir šiuolaikinės simbolinės modalinės logikos santykį. Straipsnyje tiriama Buridano modalinės silogistikos pagrindą sudarančių teiginių semantinė interpretacija ir tarp šių teiginių galiojantys išvedimo ryšiai. Pirmiausia aptariami išvedimai tarp būtinumo, galimumo, atsitiktinumo ir neatsitiktinumo teiginių (su ir be frazės quod est), kurie yra logiškai taisyklingi pagal Buridano aprašytą semantiką. Pateikiama išsami diagraminė visų išvedimo sąryšių reprezentacija. Siekiant nustatyti, ar esama tinkamo būdo Buridano gaunamus rezultatus išreikšti predikatų logikoje su modalumais, aptariamos trys literatūroje aptinkamos Buridano teiginių formalizacijos versijos. Palyginus taisyklingus išvedimus tarp kvantifikuotų formulių ir tarp Buridano modalinių teiginių, galima tvirtinti, kad Buridano teiginių semantika ir galiojantys tiesioginiai išvedimai gali būti adekvačiai perteikiami predikatų logikos su aletiniais modalumais (sistemos T) priemonėmis.
Pagrindiniai žodžiai: Jonas Buridanas, modalinė silogistika, modalinė predikatų logika, galimų pasaulių semantika
Acknowledgement.This research has received funding from the Research Council of Lithuania (LMTLT), project agreement No. S-MIP-19-51.
_________
Received: 07/02/2022. Accepted: 10/04/2022
Copyright © Jonas Dagys, Živilė Pabijutaitė, Haroldas Giedra, 2022. Published by Vilnius University Press.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Introduction
The theory of modal syllogisms provided by 14th century logician John Buridan is among the pinnacle achievements of the medieval logica moderna. More recently it has attracted increasing attention of historians of medieval logic. Initiated by Peter King (1985) and George E. Hughes (1989), more extensive research has been carried out and published most notably by Henrik Lagerlund (2000), Gyula Klima (2001, 2008), Paul Thom (2003), Juan Manuel Campos Benítez (2010), Stephen Read (2012), and Spencer Johnston (2015). Probably the interest has been, at least in part, stimulated by the widespread use of quantified modal logic with the apparatus of possible worlds semantics in current analytic philosophy. The encounter of traditional logic and modern symbolic logic gives rise to certain interesting questions. One of them, still seemingly unsettled, concerns precisely the relation of Buridan’s theory of modality with the more recent developments of symbolic modal logic. Is there a way to appropriate or model Buridan’s results in the first order modal logic? Or maybe, as is sometimes suggested, Buridan has implicitly relied on possible worlds semantics?
In what follows, we will focus on the semantics of and the inferential relations among the propositions that underlie Buridan’s theory of modal syllogism. We will first review the repertoire of the categorical statements involved in Buridan’s pure and mixed modal syllogisms. Then we will revise the admissible inferences among those statements and represent the system of inferential relations diagrammatically. Finally, we will venture the question whether the whole system can be adequately captured using the resources of first order modal logic. We aim to take sides in the ongoing controversy and claim that, contrary to what some researchers maintain, Buridan’s semantics of categorical statements and immediate inferences among them, when supplied with a suitable formalization, can be fully captured by the quantified modal logic.
I.
Buridan’s theory follows the Aristotelian tradition of categorical syllogism. Every proposition in his system is thus a categorical proposition consisting of two terms – a subject and a predicate. The system contains assertoric non-modal propositions, but also the so-called divided modal propositions that may have one of the two modes of necessity or possibility; in addition to those, there are statements of contingency and non-contingency; and each of the modal propositions could have the supposition of their subject term (more details on this below) ampliated to the possible or restricted only to the actual.
Each assertoric non-modal proposition contains two terms that are joined by a copula expressed by the relevant form of the verb “to be” (singular – est, plural – sunt; however, Buridan sometimes avoids the explicit formulation of a copula and tends to express the predicate as a verb (for instance, ‘The man runs’ (homo currit) instead of ’The man is someone who runs’ (homo est currens) (cf. SD I.3.2)1. All propositions fall into two complementary classes, according to their so-called quality, of affirmative or negative propositions. Also, the propositions have their quantity standardly expressed by the words “All” (omnis, quilibet, uterque) or “Some” (aliquid, quidam, alter, reliquus) (cf. SD I.3.5). All propositions fall into two complementary classes, according to their so-called quantity, of universal and particular propositions. As the two divisions – according to the quality and quantity – are orthogonal, four distinct propositional forms are possible. According to the nomenclature adopted by medieval logicians,2 the four types of propositions are commonly labelled by Latin vowels a, e, i, o. The two universal propositions are a and e, the two particular propositions are i and o; the two affirmative propositions are a and i; the two negative propositions are e and o. We will adopt the convention of using the upper-case X prefixed to the lower-case Latin vowel to refer to assertoric non-modal categorical types of propositions, hence in what follows they will be labelled as Xa, Xe, Xi, and Xo.
For the semantics of those propositions Buridan adopts the identity theory of predication (see, e.g. Klima 2009: 145), which is based on medieval understanding of supposition of terms. The affirmative proposition is true if all or some of the things for which the subject term supposits are identical with the things for which the predicate term supposits. And the negative propositions are true if all or some of the things fail to be identical with any of the things for which the predicate term supposits. We could state the truth conditions for the four assertoric proposition types as follows. The universal affirmative (Xa) is true if each of the things actually falling under the subject term is identical with the things actually falling under the predicate term, and the particular affirmative (Xi) is true if some of the things actually falling under the subject term is identical with the things actually falling under the predicate term. The universal negative (Xe) is true if none of the things actually falling under the subject term are identical with any of the things that actually fall under the predicate term, and the particular negative (Xo) is true if not all of the things that actually fall under the subject term are identical with the things actually falling under the predicate term. From this it also follows that the affirmative but not the negative propositions are taken to have existential import. It further follows that there are only two direct valid inferences among those four assertoric propositions – Xa implies Xi, and Xe implies Xo – the familiar pairs of subalternation (cf. SD I.4.4).
Corresponding to the four assertoric propositions, there are divided modal propositions (modales divisae). The divided modal propositions have the modes of necessity or possibility modifying their copula. Thus, we get eight more forms of propositions: four types of propositions of necessity and four types of propositions of possibility. We will adopt the convention of using the upper-case L prefixed to the Latin vowel for propositions of necessity (hence La, Le, Li, and Lo), and the upper-case M for the propositions of possibility (hence Ma, Me, Mi, and Mo). In terms of semantics, the mode immediately affects the supposition of the predicate term – the predicate term in the propositions of possibility is taken to supposit not only for the things that actually fall under the term, but also for the possible things that possibly fall under that term; in the propositions of necessity the predicate term is taken to supposit for the things that fall under the term necessarily. Buridan also says that in all divided modal propositions the subject term is ampliated to stand for possible things that actually or possibly fall under that term.
Buridan notes that each proposition of necessity implies the corresponding proposition of possibility (cf. SD I.8.6). However, where the relation of modal propositions with the assertoric propositions is concerned, the differences in supposition of terms, especially that of the subject, is now reflected in the admissible inference patterns. Despite the fact that Buridan acknowledges the intermodal principles that what is necessary is actual (cf. TC IV.1.7), and what is actual is possible, in his semantics no divided statement of necessity entails the corresponding assertoric proposition, except for the universal negative of necessity, which entails the assertoric universal negative (Le implies Xe); and also no statement of possibility is entailed by the corresponding assertoric statement, except for the particular affirmative of possibility which is implied by the assertoric particular affirmative (Xi implies Mi) (cf. TC II.6.3-4).
In addition to pure divided modals, Buridan also discusses modal propositions that have the supposition of their subject term restricted to the actual (or, we could say – the ampliation to the possible prevented) by the phrase quod est to the subject (cf. TC II.6). In these propositions the supposition of the subject term is the same as in the assertoric propositions, and the supposition of the predicate term is the same as is in the corresponding pure modal propositions. We will indicate the quod est restriction by prefixing the upper-case Q to the proposition label (hence QLa, QMe, etc.). The truth conditions for the modal propositions with quod est restriction are analogous to the truth conditions of the corresponding pure modals listed above, with one minor but significant difference – the subject term is now taken to stand only for the actual individuals falling under that term.
How do the modal propositions with quod est fit into the overall system of inferences among the assertoric and pure modal propositions? First, since the supposition of the subject term in the modal propositions with quod est is the same as in the assertoric propositions, all standard intermodal inferences are available. Thus, every proposition of necessity with quod est entails the corresponding assertoric proposition (QLa implies Xa, QLe implies Xe, QLi implies Xi, and QLo implies Xo), and every assertoric proposition entails the corresponding proposition of possibility with quodest (Xa implies QMa, Xe implies QMe, Xi implies QMi, and Xo implies QMo). However, since the supposition of the subject term in the modal propositions with quod est is not ampliated, and thus is not the same as in the purely modal propositions where it is ampliated to the possible, there is only a limited range of inferences between the pure modal propositions and the corresponding modal propositions with quod est. Among universal propositions, only the negative modals with quod est are entailed by the corresponding pure modals (Le implies QLe, Me implies QMe); and among the particular propositions, only the affirmative modals with quod est entail the corresponding pure modals (QLi implies Li, and QMi implies Mi). There are no inferences in any direction between the universal affirmatives or particular negatives with quod est and the corresponding pure modals. However, although Buridan does not discuss this, the semantics implicitly supports the inference of the universal affirmative modals with quod est from the corresponding statements without quod est, when the actual existence of individuals under the subject term is assumed (when the subject is known to be actually non-empty, La implies QLa, and Ma implies QMa).
In addition to the propositions of possibility and of necessity, Buridan also considers propositions of contingency and non-contingency. The propositions of contingency, also called contingent both ways (ad utrumlibet (cf. SD I.8.5)), are modal propositions that express the idea that whatever is designated by the subject falls under the predicate term possibly, but not necessarily. This way the proposition of contingency implies both affirmative and negative propositions of possibility, and so the quality of the contingency proposition is effectively irrelevant. Using the uppercase C to designate the propositions of contingency, we can then say that, despite their verbal differences in natural language, Ca is equivalent to Ce, and each of them implies both Ma and Me, and Ci is equivalent to Co, while each of them implies both Mi and Mo. Accordingly, the non-contingency propositions express the idea that for whatever is designated by the subject term it is either necessary or impossible to fall under the predicate term. We will designate non-contingency propositions by upper-case N. Again, Na is equivalent to Ne, and Ni to No. A universal proposition of contingency then contradicts the particular of non-contingency, and the particular of contingency contradicts the universal of non-contingency. The proposition of non-contingency is implied by any of the corresponding propositions of necessity (Na is implied by La and also by Le; Ni is implied by Li, and also by Lo) (cf. TC IV.6.7). By default propositions of contingency and non-contingency have their subject term ampliated to the possible, but restricted versions (QCa, QNi, etc.) are also possible.
II.
The system of inferences described above constitutes a significant part of the basis for Buridan’s theory of modal syllogism. In his works Buridan specifically discusses modal syllogisms that have as their premises and conclusions pure propositions of possibility, necessity or contingency, also their restricted versions or assertoric propositions can be mixed in.
Buridan has introduced a famous and widely reproduced octagon of modal propositions, whereby the system of relationships among the purely modal propositions is represented graphically on a plane. Graphic representation of those relations is a useful tool, a particularly helpful aid to human comprehension of the system. However, Buridan’s octagon, as its name reveals, includes only eight purely modal propositions. The assertoric propositions or propositions of contingency are left out, as well as the propositions with restricted ampliation of the subject.
It is thus worthwhile to provide a comprehensive and complete graphic representation of inferential relations among those statements. It is one of the aims of this paper to propose a graphic and comprehensive representation of the entire system of inferences among Buridan’s modal propositions.
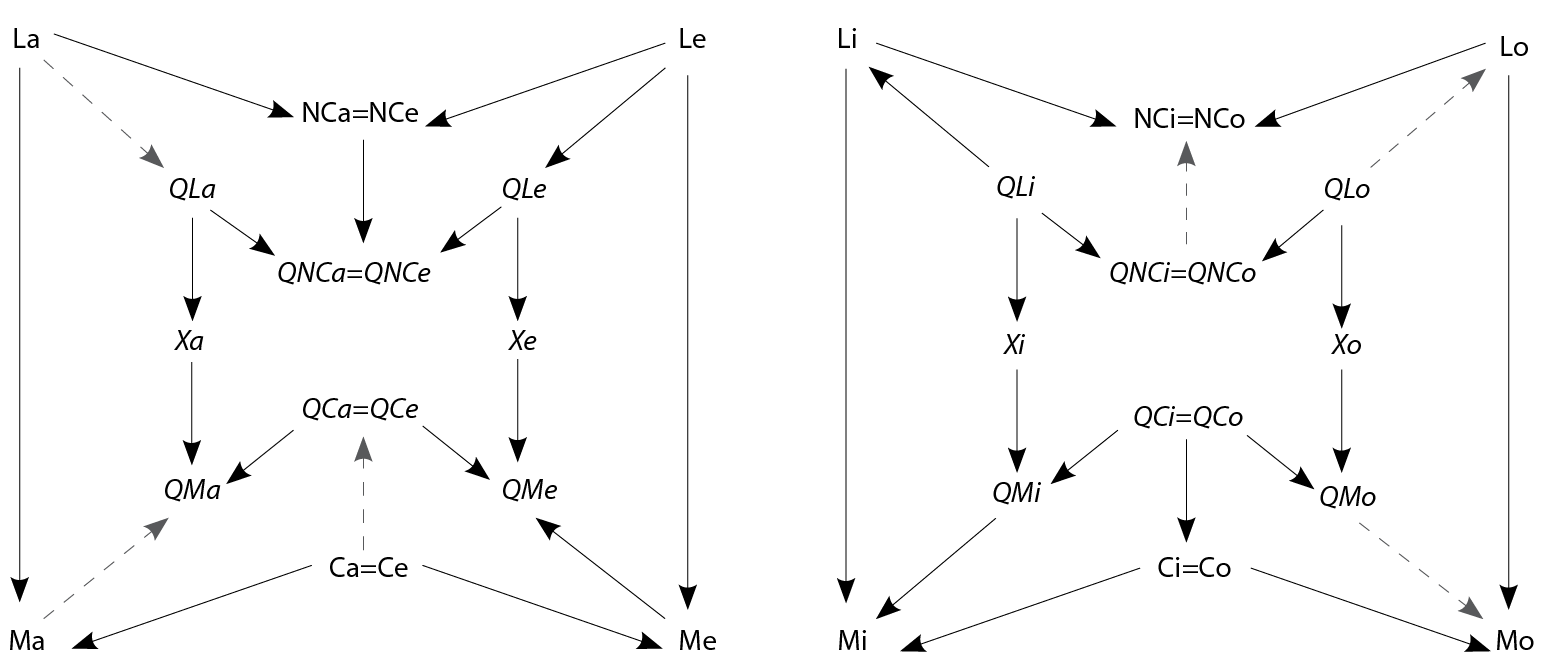 The result is a two-layered scheme. Each layer is a square that contains fourteen propositional types, connected in each by seventeen solid and three dotted arrows that represent valid inferences. Solid lines represent inferences valid in Buridan’s semantics, and dotted lines represent those inferences that are valid only if non-emptiness of a subject term is assumed or established.One square contains all kinds of universal propositions, the other – all particulars. The propositions are arranged so that a proposition of the same quality and modality is in the same place in both, so if the two squares are overlaid, the universal propositions would be mapped onto corresponding particular propositions. What is left only implicit and is not explicitly represented for purposes of simplicity (due to two dimensions), is that each of the fourteen universal propositions implies the corresponding particular of the same modality and quality.
The result is a two-layered scheme. Each layer is a square that contains fourteen propositional types, connected in each by seventeen solid and three dotted arrows that represent valid inferences. Solid lines represent inferences valid in Buridan’s semantics, and dotted lines represent those inferences that are valid only if non-emptiness of a subject term is assumed or established.One square contains all kinds of universal propositions, the other – all particulars. The propositions are arranged so that a proposition of the same quality and modality is in the same place in both, so if the two squares are overlaid, the universal propositions would be mapped onto corresponding particular propositions. What is left only implicit and is not explicitly represented for purposes of simplicity (due to two dimensions), is that each of the fourteen universal propositions implies the corresponding particular of the same modality and quality.
It may be worth noting that since each of the particular statements is a contradictory of one of the universals, every arrow in the right-hand part of the diagram can be construed as a contrapositive of some arrow in the left-hand diagram, and vice versa.
III.
Given the representation of these inferential relations, a question now may be raised whether these relations can be completely captured by any of the modern modal systems? The question is two-fold – is it possible to supply the formalizations for the statements in quantified modal logic, that would be semantically adequate and support the valid inferential relations described by Buridan? We will argue for an affirmative answer.
We have discussed the question of representing Buridan’s divided modal statements in more detail elsewhere (see Dagys et al. 2021). Here we will only list three sets of formulas available in the literature in order to see how they support the inference system that is presented in the above diagram derived from Buridan’s semantics.
In the introduction to his own translation of Buridan’s Treatise on Consequence, Stephen Read suggests the following formalizations for the eight propositions in Buridan’s modal octagon (Read 2015: 40) and also the contingency and non-contingency propositions (ibid., 49):
|
La |
∀x (◇Sx → □Px) ∧ ∃x ◇Sx |
|
Le |
∀x (◇Sx → □¬Px) |
|
Li |
∃x (◇Sx ∧ □Px) |
|
Lo |
∃x (◇Sx ∧ □¬Px) ∨ ¬∃x ◇Sx |
|
Ma |
∀x (◇Sx → ◇Px) ∧ ∃x ◇Sx |
|
Me |
∀x (◇Sx → ◇¬Px) |
|
Mi |
∃x (◇Sx ∧ ◇Px) |
|
Mo |
∃x (◇Sx ∧ ◇¬Px) ∨ ¬∃x ◇Sx |
|
Ca/Ce |
∀x (◇Sx → (◇Px ∧ ◇¬Px)) ∧ ∃x ◇Sx |
|
Ci/Co |
∃x (◇Sx ∧ (◇Px ∧ ◇¬Px)) |
|
Na/Ne |
∀x (◇Sx → ¬(◇Px ∧ ◇¬Px)) |
|
Ni/No |
∃x (◇Sx ∧ ¬(◇Px ∧ ◇¬Px)) ∨ ¬∃x ◇Sx |
Read does not list the formulas for the propositions with quod est, but their formalization can presumably be achieved by simply removing the diamond operator from each occurrence of Sx, which represents the subject term. We thereby get the formulas for the quod est propositions.
|
QLa |
∀x (Sx → □Px) ∧ ∃x Sx |
|
QLe |
∀x (Sx → □¬Px) |
|
QLi |
∃x (Sx ∧ □Px) |
|
QLo |
∃x (Sx ∧ □¬Px) ∨ ¬∃x Sx |
|
QMa |
∀x (Sx → ◇Px) ∧ ∃x Sx |
|
QMe |
∀x (Sx → ◇¬Px) |
|
QMi |
∃x (Sx ∧ ◇Px) |
|
QMo |
∃x (Sx ∧ ◇¬Px) ∨ ¬∃x Sx |
|
QCa/QCe |
∀x (Sx → (◇Px ∧ ◇¬Px)) ∧ ∃x Sx |
|
QCi/QCo |
∃x (Sx ∧ (◇Px ∧ ◇¬Px)) |
|
QNa/QNe |
∀x (Sx → ¬(◇Px ∧ ◇¬Px)) |
|
QNi/QNo |
∃x (Sx ∧ ¬(◇Px ∧ ◇¬Px)) ∨ ¬∃x Sx |
Read’s formulas are the least complex of the three sets, in that they seem to operate in the system of world invariant domain, and they also ignore any complications around the question how true predication is related to existence in Buridan’s semantics. One way of expressing more sensitivity to the latter issue is represented by the formulas provided by Spencer Johnston. Some formulas are explicitly provided in the paper by Hodges and Johnston (2017), where they use the proposition function Ox to represent the dedicated predicate of existence at a world. They only provide the example of the formula for La, but following the semantic reconstruction provided by Johnston (2015) the complete list of formulas for the modal propositions can be reconstructed as follows:
|
La |
∀x (◇(Ox ∧ Sx) → □(Ox ∧ Px)) ∧ ∃x ◇(Ox ∧ Sx) |
|
Le |
∀x (◇(Ox ∧ Sx) → □¬(Ox ∧ Px)) |
|
Li |
∃x (◇(Ox ∧ Sx) ∧ □(Ox ∧ Px)) |
|
Lo |
∃x (◇(Ox ∧ Sx) ∧ □¬(Ox ∧ Px)) ∨ ¬∃x ◇(Ox ∧ Sx) |
|
Ma |
∀x (◇(Ox ∧ Sx) → ◇(Ox ∧ Px)) ∧ ∃x ◇(Ox∧Sx) |
|
Me |
∀x (◇(Ox ∧ Sx) → ◇¬(Ox ∧ Px)) |
|
Mi |
∃x (◇(Ox ∧ Sx) ∧ ◇(Ox ∧ Px)) |
|
Mo |
∃x (◇(Ox ∧ Sx) ∧ ◇¬(Ox ∧ Px)) ∨ ¬∃x ◇(Ox ∧ Sx) |
|
Ca/Ce |
∀x (◇(Ox ∧ Sx) → (◇(Ox ∧ Px) ∧ ◇¬(Ox ∧ Px))) ∧ ∃x ◇(Ox ∧ Sx) |
|
Ci/Co |
∃x (◇(Ox ∧ Sx) ∧ (◇(Ox ∧ Px) ∧ ◇(Ox ∧ ¬Px))) |
|
Na/Ne |
∀x (◇(Ox ∧ Sx) → ¬(◇(Ox ∧ Px) ∧ ◇¬(Ox ∧ Px))) |
|
Ni/No |
∃x (◇(Ox ∧ Sx) ∧ ¬(◇(Ox ∧ Px) ∧ ◇¬(Ox ∧ Px))) ∨ ¬∃x ◇(Ox ∧ Sx) |
The set of formulas for the corresponding quod est propositions are not listed, but again they can be easily achieved by removing the diamond operator flanking occurrences of Sx, which represents the subject term.
|
QLa |
∀x ((Ox ∧ Sx) → □(Ox ∧ Px)) ∧ ∃x (Ox ∧ Sx) |
|
QLe |
∀x ((Ox ∧ Sx) → □¬(Ox ∧ Px)) |
|
QLi |
∃x ((Ox ∧ Sx) ∧ □(Ox ∧ Px)) |
|
QLo |
∃x ((Ox ∧ Sx) ∧ □¬(Ox ∧ Px)) ∨ ¬∃x (Ox ∧ Sx) |
|
QMa |
∀x ((Ox ∧ Sx) → ◇(Ox ∧ Px)) ∧ ∃x (Ox ∧ Sx) |
|
QMe |
∀x ((Ox ∧ Sx) → ◇¬(Ox ∧ Px)) |
|
QMi |
∃x ((Ox ∧ Sx) ∧ ◇(Ox ∧ Px)) |
|
QMo |
∃x ((Ox ∧ Sx) ∧ ◇¬(Ox ∧ Px)) ∨ ¬∃x (Ox ∧ Sx) |
|
QCa/QCe |
∀x ((Ox ∧ Sx) → (◇(Ox ∧ Px) ∧ ◇¬(Ox ∧ Px))) ∧ ∃x (Ox ∧ Sx) |
|
QCi/QCo |
∃x ((Ox ∧ Sx) ∧ (◇(Ox ∧ Px) ∧ ◇(Ox ∧ ¬Px))) |
|
QNa/QNe |
∀x ((Ox ∧ Sx) → ¬(◇(Ox ∧ Px) ∧ ◇¬(Ox ∧ Px))) |
|
QNi/QNo |
∃x ((Ox ∧ Sx) ∧ ¬(◇(Ox ∧ Px) ∧ ◇¬(Ox ∧ Px))) ∨ ¬∃x (Ox ∧ Sx) |
It is worth noting that both Read’s and Johnston’s formalization is based on the semantics for the affirmatives of necessity (and correspondingly for the negatives of possibility) that is explicitly endorsed in the text of Buridan’s Summulae de dialectica, whereby the necessary affirmative predication entails necessary existence. This is a particularly strong semantics for the affirmatives of necessity, as it renders all instances of necessary affirmatives about contingent beings simply false, and all corresponding instances of possibility negatives simply true. As a result, only very few concepts (if not just one, namely – “God”), can be used as predicates in true affirmatives of necessity. This treatment is consistent with Buridan’s examples. However, in the Treatise on Consequences and also in Quaestiones in analytica priora, Buridan hints at the possibility of slightly weaker semantics for propositions of necessity, whereby necessary predication is taken to be true in cases where the objects involved have the predicate as long as they exist. He calls it “conditional necessity” (necessitas conditionalis). Hence, a third set of formulas might be suggested, where the formalization of the necessary affirmatives suggested by Johnston3 are modified to have a form of the conditional, and where the negatives of possibility are modified accordingly. Since the possibility affirmatives and necessity negatives are not affected by this modification and remain exactly as listed in the formalization we have attributed to Johnston, we do not list them here.
|
La |
∀x (◇(Ox ∧ Sx) → □(Ox → Px)) ∧ ∃x ◇(Ox ∧ Sx) |
|
Li |
∃x (◇(Ox ∧ Sx) ∧ □(Ox → Px)) |
|
Me |
∀x (◇(Ox ∧ Sx) → ◇(Ox ∧ ¬Px)) |
|
Mo |
∃x (◇(Ox ∧ Sx) ∧ ◇(Ox ∧ ¬Px)) ∨ ¬∃x ◇(Ox ∧ Sx) |
The corresponding quod est propositions would again be achieved by removing the diamond flanking Sx.
|
QLa |
∀x ((Ox ∧ Sx) → □(Ox → Px)) ∧ ∃x (Ox ∧ Sx) |
|
QLi |
∃x ((Ox ∧ Sx) ∧ □(Ox → Px)) |
|
QMe |
∀x ((Ox ∧ Sx) → ◇(Ox ∧ ¬Px)) |
|
QMo |
∃x ((Ox ∧ Sx) ∧ ◇(Ox ∧ ¬Px)) ∨ ¬∃x (Ox ∧ Sx) |
The significant result is that despite certain syntactic and semantics differences, as far as the inferential relations among propositions are concerned, all three ways of formalization provide identical results – all inferences that are valid according to Buridan’s semantics are also valid in quantified modal logic as simple as T. The inferences from propositions of necessity to corresponding propositions of non-contingency as well as inferences from propositions of contingency to corresponding propositions of possibility are validated by simple first order logic. The inferences from propositions of necessity to corresponding propositions of possibility require the same with addition of the definition of possibility operator in terms of necessity and negation, which is available in any modal system based on propositional K. All other inferences require to add nothing more than the characteristic axiom of modal system T, namely □p→p. In terms of possible world semantics, nothing more than reflexivity is required of the accessibility relation among worlds. Proof theoretic analysis of inferential relations among the listed formulas reveals that quantified logic based on propositional T is sound and complete with regard to inferences based on Buridan’s semantics4. More precisely, every inference valid in Buridan’s semantics is valid in quantified T, and each of the inferences among the listed formulas that is valid in quantified T is also valid in Buridan’s semantics. This means that proof theoretic methods of quantified modal logic are sound and complete with regard to a significant fragment of Buridan’s modal logic, when supplied with a suitable formalization. It is important to realize that claiming this, however, does not amount to the claim that quantified modal logic or possible world semantics is implicit in Buridan’s theory, as is sometimes suggested (e.g., by Hughes 1989: 97). It is not even clear, what would be required to support that claim. It seems that the sole modal principle that Buridan’s semantics relies upon, namely, that whatever is necessary is actual (and, by contraposition, whatever is actual is possible) can be given a rather simple set theoretic account that does not require even implicit use of possible worlds machinery. That notwithstanding, Buridan’s system, as far as inferences among various modal propositions are concerned, is provably capable of being fully represented when possible worlds semantics is used.
This result might also be taken as an early indication that Buridan’s modal syllogistic could be entirely captured by quantified modal logic, but a more thorough analysis is required to substantiate the latter claim, and this is what we will eventually undertake in the nearest future.
Conclusions
1. After reviewing the categorical propositions involved in Buridan’s pure and mixed modal syllogisms and revising the admissible inferences among those statements, we have represented Buridan’s system of inferential relations diagrammatically and have listed three different ways of formalization of Buridan’s modal statements – provided by Stephen Read, Spencer Johnston and the authors of this article.
2. These three ways of representing Buridan’s modal propositions, although having syntactic and semantical differences, have lead us to the same conclusion – all the inferences valid in Buridan’s semantics can be shown to be valid in the quantified modal system T. So, quantified modal T is sound and complete with regard to Buridan’s semantics as far the inferences between modal propositions are concerned.
3. We also claim that this result is probably too weak to support the hypothesis advanced by some historians of logic, that possible world semantics is implicit in Buridan’s theory. Although the only modal principle required by Buridan’s semantics can be expressed by the characteristic axiom of modal system T, it can be explained by less complex set theoretic relations.
References
Buridan, J., 2001. Summulae de Dialectica. An annotated translation with a philosophical introduction by Gyula Klima. New Haven: Yale University Press.
Buridan, J., 2015. Treatise on Consequences. Translated and with an introduction by Stephen Read. New York: Fordham University Press.
Buridan, J., n.d. Sinne anno. Quaestiones in Analytica priora. Unpublished typescript edited by H. Hubien, partially available at https://www.logicmuseum.com/wiki/Authors/Buridan/Quaestiones_in_analytica_priora
Campos Benítez, J. M., 2010. La conversión modal medieval y el sistema modal S5 de Lewis, in A. Eichmann Oehrli and M. Frías Infante (eds.), Classica Boliviana: Actas del V Encuentro Boliviano de Estudios Clásicos. La Paz: Plural Editores, 123–141.
Dagys, J., Pabijutaitė, Ž., and Giedra, H., 2021. Representing Buridan’s Divided Modal Propositions in First-Order Logic. History and Philosophy of Logic, DOI: 10.1080/01445340.2021.1976042
Hodges, W., and Johnston, S., 2017. Medieval Modalities and Modern Method: Avicenna and Buridan. IfCoLog Journal of Logics and their Applications 4(4): 1029–1073.
Hughes, G., 1989. The modal logic of John Buridan. In G. Corsi, C. Mangione, and M. Massimo, Atti del Convegno Internationale di Storia della Logica: Le teorie delle modalita. Bologna: Editrice Cooperativa Libraria Universitaria Editrice, 93–111.
Johnston, S., 2015. A formal Reconstruction of Buridan’s Modal Syllogism. History and Philosophy of Logic 36(1): 2-17, DOI: 10.1080/01445340.2014.934090
King, P., 1985. Jean Buridan’s Logic: The Treatise on Supposition The Treatise on Consequences. Dordrecht/ Boston/ Lancaster/ Tokyo: D. Reidel Publishing Company.
Klima, G., 2001. Existence and Reference in Medieval Logic. In E. Morscher, A. Hieke (eds), New Essays in Free Logic. Applied Logic Series, vol 23. Springer, Dordrecht, 197-226. https://doi.org/10.1007/978-94-015-9761-6_10
Klima, G., 2009. John Buridan. Oxford-New York: Oxford University Press.
Lagerlund, H., 2000. Modal Syllogistics in the Middle Ages, Leiden: Brill.
Read, S., 2012. John Buridan’s Theory of Consequence and his Octagons of Opposition. In J.-Y. Beziau & Dale Jacquette (eds.), Around and Beyond the Square of Opposition. Birkhäuser, 93—110.
Read, S., 2015. Introduction. In J. Buridan, Treatise on Consequences, New York: Fordham University Press, 1-52.
Thom, P., 2003. Medieval Modal Systems. Problems and Concepts. Aldershot: Ashgate.
1 References to Buridan’s original texts are to be given by indicating the abbreviated title and section of the work. SD stands for Summulae de dialectica, and TC for Tractatus de consequentiis.
2 It may be worth mentioning as a side-note that there is no explicit mention of these abbreviations in Buridan‘s original texts, and he always refers to the propositional types by their full names. But the abbreviations must have been familiar to him, as they are implicit in the traditional names of syllogistic forms, like Barbara, Celarent, etc., which are used by Buridan.
3 No such modifications are available to Read‘s formalizations, since the connection between existence and predication is not explicitly represented there.
4 Those willing to check the details might want to appreciate the help of automated proof engines, such as Tree proof generator created by Wolfgang Schwartz, available at https://www.umsu.de/trees/.